3  Analyse Factorielle des Correspondances (AFC)

L’Analyse Factorielle des Correspondances (AFC) est une méthode d’analyse des tables de contingence obtenues à partir des données de deux variables qualitatives \(X\) et \(Y\) sur \(n\) individus. Notons

\[ \begin{aligned} X(\Omega) &= \{a_1, \ldots, a_{k},\cdots , a_K\}\\ Y(\Omega) &= \{b_1, \ldots, b_{l},\cdots, b_L\},\\ \end{aligned} \]

les ensembles des modalités de \(X\) et \(Y\) respectivement.

Les données sont en général résumées dans une table de contingence :

	\(b_1\)	\(\cdots\)	\(b_{l}\)	\(\cdots\)	\(b_L\)	Total
\(a_1\)	\(n_{1,1}\)	\(\cdots\)	\(n_{1,l}\)	\(\cdots\)	\(n_{1,L}\)	\(n_{1,+}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(a_k\)	\(n_{k,1}\)	\(\cdots\)	\(n_{k,l}\)	\(\cdots\)	\(n_{k, L}\)	\(n_{k, +}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(a_K\)	\(n_{K, 1}\)	\(\cdots\)	\(n_{K,l}\)	\(\cdots\)	\(n_{K, L}\)	\(n_{K, +}\)
Total	\(n_{+,1}\)	\(\cdots\)	\(n_{+, l}\)	\(\cdots\)	\(n_{+,L}\)	\(n\)

• \(n_{k,l}\) est l’effectif du couple \((a_k, b_l)\)
• \(n_{k,+}=\sum_{l=1}^Ln_{k, l}\) est l’effectif marginal de \(a_k\)
• \(n_{+, l}=\sum_{k=1}^Kn_{k,l}\) est l’effectif marginal de \(b_l\).

Objectif: Investiguer les correspondances entre les modalités des deux variables.

3.1 Quelques statistiques

3.1.1 Fréquences

Definition 3.1  

• Fréquence du couple \((a_k, b_l)\)

\[ f_{k,l}=\dfrac{n_{k,l}}{n} \]

• Fréquence marginale de \(a_k\) \[ f_{k,+}=\dfrac{n_{k,+}}{n}=\sum_{l=1}^Lf_{k,l} \]

• Fréquence marginale de \(b_l\) \[ f_{+,l}=\dfrac{n_{+,l}}{n}=\sum_{k=1}^Kf_{k,l} \]

3.1.2 Test du chi carré d’indépendance

Il permet de tester \[ \mathcal{H}_0:\quad X \text{ et } Y \text{ sont indépendantes} \] contre \[ \mathcal{H}_1:\quad X\text{ et }Y\text{ sont liées}. \] Effectifs attendus sous \(\mathcal{H}_0\)

\[ \widehat{n}_{k,l}=\dfrac{n_{k,+}n_{+,l}}{n} \]

Statistique de test

\[ \begin{aligned} \mathbb{X}^2&=\sum_{k=1}^K\sum_{l=1}^L\dfrac{\left(n_{k,l}-\widehat{n}_{k,l}\right)^2}{\widehat{n}_{k,l}}\\ &\overset{\mathcal{H}_0}{\rightarrow}\chi_{(K-1)(L-1)}^2 \end{aligned} \]

Valeur \(p\)

\[ pValue = \mathbb{P}\left(\chi_{(K-1)(L-1)}^2>\mathbb{X}_{obs}^2\right) \]

Décision au niveau \(\alpha\)

On rejette \(\mathcal{H_0}\) si et seulement si:

• \(\mathbb{X}_{obs}^2>q_{1-\alpha}\left(\chi_{(K-1)(L-1)}^2\right)\) ou de façon équivalente

• \(pValue<\alpha\)

Note

• Lorsque le test est significatif, il il devient alors pertinent de s’intéresser aux correspondances entre les modalités des deux variables.

Remarque

• Le test est non significatif lorsque \[ \dfrac{n_{k, l}}{n_{k,+}}\approx\dfrac{n_{+,l}}{n},\quad \forall k,l \]

ou de façon équivalente

\[ \dfrac{n_{k, l}}{n_{+,l}}\approx\dfrac{n_{k,+}}{n},\quad \forall k,l. \]

• L’indépendance entre les deux variables correspond alors à la situation où le nuage des profils lignes (ou colonnes) est concentré autour d’un point.

3.1.3 Nuages de profils

Notations et definitions

• \(N=\left(n_{k,l}\right)_{k=1,\cdots,K;l=1,\cdots,L}\) la matrice de contingence;

• \(D_r=diag\left(n_{k,+}\right)_{k=1}^K\) matrice des effectifs marginaux de \(X\);

• \(D_c=diag\left(n_{+, l}\right)_{l=1}^L\) matrice des effectifs marginaux de \(Y\);

• \(f_{k,+}=\dfrac{n_{k,+}}{n}\) la fréquence marginale de la modalité \(a_k\) de \(X\);

• \(f_{+,l}=\dfrac{n_{+,l}}{n}\) la fréquence marginale de la modélité \(b_l\) de \(Y\);

Definition 3.2 (Nuage des profils lignes)  

• Profil de la ligne \(k\): \[L_k=\left(\dfrac{n_{k,l}}{n_{k,+}}\right)_{l=1}^L\in\mathbb{R}^L\]

• Nuage des profils-lignes:

\[ \mathcal{N}_r=\left\{\left(L_k, f_{k,+}\right)\right\} \]

Definition 3.3 (Nuage des profils colonnes)  

• Profil de la colonne \(l\): \[ C_l=\left(\dfrac{n_{k,l}}{n_{+,l}}\right)_{k=1}^K\in\mathbb{R}^K \]

• Nuage des profils-colonnes: \[ \mathcal{N}_c=\left\{\left(C_l, f_{+, l}\right)\right\} \]

Considérons les matrices suivantes des profils:

\[ T_r=\begin{bmatrix} {}^tL_1\\ \vdots\\ {}^tL_K \end{bmatrix}\in\mathbb{R}^{K\times L} \]

\[ T_c = \begin{bmatrix} C_1 & \cdots & C_L \end{bmatrix}\mathbb{R}^{K\times L}. \]

Proposition 3.1 (Matrices des profils)  

• \(T_r=D_r^{-1}N\)

• \(T_c = ND_c^{-1}\)

Proposition 3.2 (Les centres de gravités) Les centres de gravités des nuages \(\mathcal{N}_r\) et \(\mathcal{N}_c\) sont respectivement: \[ g_r=\left(f_{+,l}\right)_{l=1}^L\in\mathbb{R}^L \] et \[ g_c=\left(f_{k,+}\right)_{k=1}^K\in\mathbb{R}^K. \]

Proof 3.4 (En exercice.).

3.2 Espaces métriques des profils

3.2.1 Métrique sur l’espace des profils lignes

Sur l’espace des profiles lignes, on considère le produit scalaire défini par la métrics \[ M = nD_c^{-1} \]

Exercise 3.1  

• Montrer que la distance associée à \(M\) est donnée par \[ d_M^2\left(L_{k}, L_{k'}\right)=\sum_{l=1}^L\dfrac{n}{n_{+,l}}\left(\dfrac{n_{k,l}}{n_{k,+}}-\dfrac{n_{k',l}}{n_{k',+}}\right)^2 \]

Definition 3.4 (Métrique de \(\chi^2\)) La métrique définie par \(M\) est encore appelée métrique du \(\chi^2\) et la distance associée notée \(d_{\chi^2}\).

3.2.2 Métrique sur l’espace des profils colonnes

Sur l’espace des profiles lignes, on considère le produit scalaire défini par la métrics \[ M = nD_r^{-1} \]

Exercise 3.2  

• Montrer que la distance associée à \(M\) est donnée par \[ d_M^2\left(C_{l}, C_{l'}\right)=\sum_{k=1}^K\dfrac{n}{n_{k,+}}\left(\dfrac{n_{k,l}}{n_{+,l}}-\dfrac{k,l'}{n_{+,l'}}\right)^2 \]

3.2.3 Inertie

Definition 3.5 (Inertie du nuage des profils-lignes \(\mathcal{N}_r\)) \[ I\left(\mathcal{N}_r\right)=\sum_{k=1}^Kf_{k,+}d_{\chi^2}^2\left(L_k, g_r\right) \]

Definition 3.6 (Inertie du nuage des profils-colonnes \(\mathcal{N}_c\)) \[ I\left(\mathcal{N}_c\right)=\sum_{l=1}^Lf_{+,l}d_{\chi^2}^2\left(C_l, g_c\right) \]

Proposition 3.3 \[ I\left(\mathcal{N}_r\right)=I\left(\mathcal{N}_c\right)=\dfrac{1}{n}\mathbb{X}^2 \]

Proof 3.4 (En exercice).

3.3 Principe de l’AFC

L’AFC est une ACP sur l’un des nuages des profiles. En effet, les les sous-sections suivantes montrent que les ACP sur les deux nuages de profils sont équivalentes.

3.3.1 ACP sur les profils lignes

3.3.1.1 Matrice à décomposée

Reppelons que, pour les données \(X\), les poids \(D\) et la métrique \(M\), l’ACP est faite sur les données centrée \(Y=X-\mathbf{1}_n{}^tg\): on la note alors ACP\((Y, D, M)\). L’ACP\((Y, D, M)\) repose sur la décomposition spectrale de la matrice \(S^2M\), où \[ S^2={}^tYDY={}^tXDX-g{}^tg \] est la matrice des variances-covariances.

Dans le cas des profiles lignes, on a: \[ \left(X, D, M\right) = \left(T_r, \dfrac{1}{n}D_r, nD_c^{-1}\right). \]

Ainsi

\[ S^2M={}^tT_rT_c-ng_r{}^tg_rD_c^{-1}. \]

Proposition 3.4 (ACP des profils lignes) Supposons que \(rg({}^tT_rT_c)=r\). Notons \(\mathcal{S}_{L-1}=\left\{\left(\pi_l\right)_{l=1}^L|\ \sum_{l=1}^L\pi_l=1\right\}\).

1. \(g_r\) est \(nD_c^{-1}\)-normé.

2. Pour tout \(x\in\mathcal{S}_{L-1}\), \((x-g_r)\perp_{nD_c^{-1}}g_r\).

3. Les matrices \({}^tT_rT_c\) et \(S^2M\) se diagonalisent dans la même base \(nD_c^{-1}\)-orthonormée.

4. \(g_r\) est un vecteur propre de \(S^2M\) associé à la valeur propre \(0\).

5. \(g_r\) est un vecteur propre de \({}^tT_rT_c\) associé à la valeur propre \(1\).

6. Les autres vecteurs propres de \(S^2M\) et \({}^tT_rT_c\) sont \(nD_c^{-1}\)-orthogonaux à \(g_r\), et sont associés aux mêmes \(r-1\) valeurs propres \(\lambda_1>\cdots>\lambda_r>0\). pour \(L\) et \(S^2M\).

Proof 3.4 (En exercice).

1. Vérifier que \(n{}^tg_rD_c^{-1}g_r=1\).

2. Montrer que pour tout \(x\in\mathcal{S}_{L-1}\), \(x-g_r\) est \(nD_c^{-1}\)-orthogonal à \(Og_r\).

3. Montrer \(ng_r{}^tg_rD_c^{-1}\) est la matrice de la projection \(nD_c^{-1}\)-orthogonale sur la droite \((Og_r)\).

4. Montrer que \(g_r\) est un vecteur propre de \(S^2M\) associé à la valeur propre \(0\).

5. Montrer que \(g_r\) est un vecteur propre de \({}^tT_rT_c\) associé à la valeur propre \(1\).

6. En déduire que tout vecteur propre de \(S^2M\) est aussi vecteur propre de \({}^tT_rT_c\) associé à la même valeur propre.

Note

• Daprès Proposition 3.4, il est inutile de centrer le tableau des profils-lignes;

• À la valeur propre \(1\) de \({}^tT_rT_c\) associée au vecteur propre \(g_r\), on fera correspondre la valeur propre \(0\) de \(S^2M\) pour se ramener à une étude centrée en \(g_r\).

3.3.1.2 Composantes principales

Notons \(\left(u^k\right)_{k=1}^{r}\) les vecteurs propres \(nD_c^{-1}\)-orthonormés de \(L\), autre que \(g_r\), rangés dans l’ordre décroissant des valeurs propres \(\lambda_1>\cdots>\lambda_{r}>0\). Posons \[ U=\begin{bmatrix} u^1 & \cdots & u^r \end{bmatrix}\in\mathbb{R}^{L\times r}, \]

et \[ \Lambda = diag\left(\lambda_k\right)_{k=1}^{r}\in\mathbb{R}^{r\times r)}. \]

La matrice des composantes principale est \[ C = nT_rD_c^{-1}U. \]

Proposition 3.5  

• Les CP sont centrées: \[\dfrac{1}{n}{}^tCD_r\mathbb{1}_K=0_K\]

• Les CP sont décorrelées est de variances les \(\lambda_k\): \[\dfrac{1}{n}{}^tCD_rC=\Lambda.\]

3.3.2 ACP sur les profils colonnes

Exercise 3.3 (ACP des profils-colonnes) Les données de l’ACP des profils-colonnes sont dans la matrice \({}^tT_c\). Ainsi nous avons à faire à l’ACP\(\left({}^tT_c, \dfrac{1}{n}D_c, nD_r^{-1}\right)\).

1. Vérifier que \(S^2M=T_c{}^tT_r-ng_c{}^tg_cD_r^{-1}\).

2. Montrer que \(g_c\) est un vecteur propre de \(S^2M\) associé à la valeur propre \(0\).

3. Montrer que \(g_c\) est un vecteur propre de \(T_c{}^tT_r\) associé à la valeur propre \(1\).

4. En déduire que l’analyse peut être faite en diagonalisant \(T_c{}^tT_r\).

5. Soit \(c^k\) la \(k\)-ième composante principale de l’ACP des profils-lignes. Montrer que \(D_rc^k\) est un vecteur propre de \(T_c{}^tT_r\).

6. Montrer que \(\|D_rc^k\|_{\chi^2}^2=n^2\lambda_k\).

7. En déduire que les vecteurs propres de \(T_r{}^tT_c\) associés aux valeurs propres \(\lambda_k\) sont les \[v^k=\dfrac{1}{\sqrt{\lambda_k}}\dfrac{n_{k,+}}{n}c^k\]

8. Montrer que la \(k\)-ième composante principale est donnée par \[\tilde{c}^k=n{}^tT_cD_r^{-1}v^k\].

3.3.3 Relations de transition

Les composantes principales des profils-lignes et celles des profils-colonnes sont reliées par des formules simples dont l’intérêt est d’éviter deux diagonalisations.

Theorem 3.1 (Relations de transition) Posons \(r=rg\left({}^tT_rT_c\right)=rg\left(T_c{}^tT_r\right)\). Alors les vecteurs propres \(u^k\) et \(v^k\) de \({}^tT_rT_c\) et \(T_c{}^tT_r\) associés à la valeur propre commune \(\lambda_k\) sont liés par les relations: \[ \begin{aligned} v^k&=\dfrac{1}{\sqrt{\lambda_k}}T_cu^k\\ u^k&=\dfrac{1}{\sqrt{\lambda_k}}{}^tT_rv^k\\ \end{aligned} \]

Proof 3.4 (En exercice).

3.3.4 Récapitulatifs

Profils lignes	Éléments	Profils colonnes
\(T_r=D_{r}^{-1}N\)	Données	\({}^tT_c=D_c^{-1}{}^tN\)
\(\dfrac{1}{n}D_r\)	Poids	\(\dfrac{1}{n}D_c\)
\(nD_c^{-1}\)	Métrique	\(nD_r^{-1}\)
\({}^tT_rT_c\)	Matrice à diagonaliser	\(T_c{}^tT_r\)
\(\lambda_1>\cdots>\lambda_r>0\)	Valeurs propres \(> 0\)	\(\lambda_1>\cdots>\lambda_r>0\)
\({}^tT_rT_cu^k=\lambda_ku^k\)	Vecteurs propres	\(T_c{}^tT_rv^k=\lambda_kv^k\)
\(u^k=\dfrac{1}{\sqrt{\lambda_k}}{}^tT_rv^k\)	Transition	\(v^k=\dfrac{1}{\sqrt{\lambda_k}}T_cu^k\)
\(c^k=nT_rD_c^{-1}u^k\)	Composantes principales	\(\widetilde{c}^k=n{}^tT_cD_r^{-1}v^k\)
\(D_rc^k=n\sqrt{\lambda_k}v^k\)		\(D_c\widetilde{c}^k=n\sqrt{\lambda_k}u^k\)

• Les éléments des ACP des profils-lignes et profils-colonnes sont reliées par des formules de transition dont l’intérêt est d’éviter deux diagonalisations.

3.3.5 Aide à l’interprétation

3.3.5.1 Analyse des Inerties

• Inertie totale : Mesure de la variabilité totale dans les données, similaire à la variance en analyse quantitative.

• Part de l’inertie expliquée en dimension \(q\) : \[\dfrac{\sum_{j=1}^q\lambda_j}{\sum_{j=1}^r\lambda_j}.\] En général, on prendra \(q=2\). Dans tous les cas, il est important d’accompagner chaque représentation de la part de l’inertie expliquée pour justifier la pertinence des conclusions qu’on peut en tirer.

3.3.5.2 Lecture des Graphiques de Points (Biplot)

• Proximité entre catégories : Les catégories proches sur le graphique sont associées positivement, c’est-à-dire qu’elles tendent à co-occurrence fréquemment.

• Opposition entre catégories : Les catégories à l’opposé du centre ont une association négative.

• Qualité de représentation :

  • Les catégories éloignées du centre sont bien représentées sur le graphique et leur position est fiable.

  • Les points proches du centre ne sont pas bien représentés et leurs positions sont moins interprétables.

3.3.5.3 Contribution des Catégories

• Les contributions des catégories aux les axes aident à identifier les catégories qui influencent le plus chaque axe.

  • Une contribution élevée signifie que la catégorie est une bonne représentante de cet axe.

• Qualité de Représentation : Le \(\cos^2\) indique la qualité de représentation d’une catégorie sur un axe factoriel.

3.4 Exemple

3.4.1 Les données

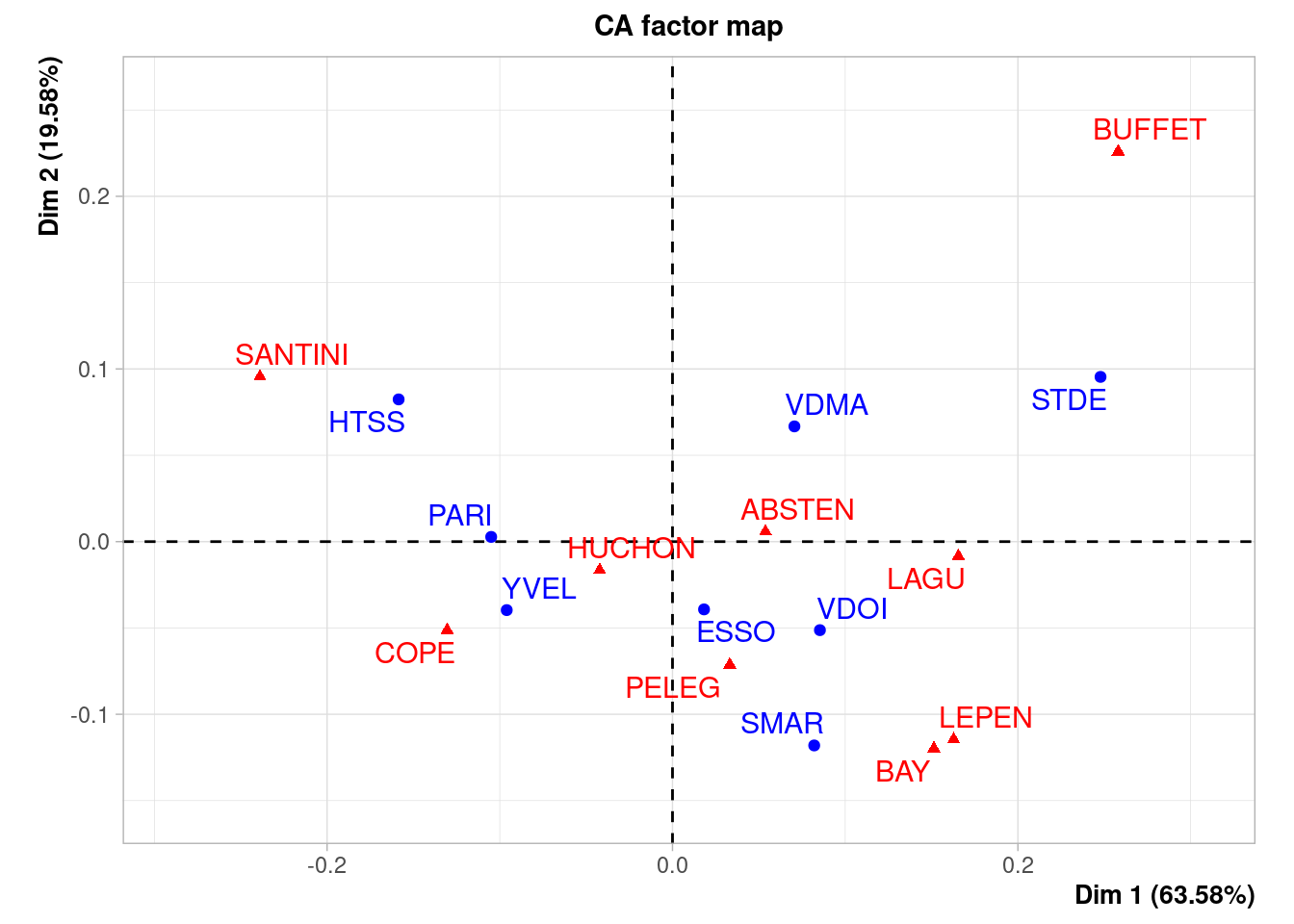
Nous considérons les données constituées par les résultats du premier tour des élections régionales de 2004 pour la région Ile de France. Pour chacun des huit départements de l’Ile de France (en lignes), on a les effectifs de suffrages pour chacune des huit listes candidates ainsi que les effectifs d’abstentions (en colonnes). L’objectif est d’analyser la structure des votes ainsi que les liaisons entre listes et départements.

require(FactoMineR)
require(ggplot2)
require(factoextra)
require(dplyr)

dfRegionales = 
  read.csv("../../data/regionales-2004-idf.csv", sep = ";")
  
row.names(dfRegionales) = dfRegionales$X

dfRegionales = dfRegionales[, -1]

dfRegionales 

3.4.2 Test d’indépendance du chi carré

chisq.test(dfRegionales)

    Pearson's Chi-squared test

data:  dfRegionales
X-squared = 146308, df = 56, p-value < 2.2e-16

Note

Au niveau \(\alpha=5\%\), il exite un lien significatif entre les listes et les localités.

3.4.3 Réalisation de l’AFC

Le package FactorMineR contient une fonction nommée CA (Canonical Analysis) permettant de faire l’AFC.

L’AFC

regionalesCA <- CA(dfRegionales, graph = FALSE)

Les fréquences marginales des lignes

regionalesCA$call$marge.row

     PARI      SMAR      YVEL      ESSO      HTSS      STDE      VDMA      VDOI 
0.1834221 0.1185859 0.1363277 0.1116021 0.1350064 0.1030204 0.1119462 0.1000891 

Les fréquences marginales des colonnes

regionalesCA$call$marge.col

     HUCHON        COPE     SANTINI       LEPEN      BUFFET        LAGU 
0.190288932 0.147663618 0.096009543 0.072996647 0.042907549 0.023759616 
      PELEG         BAY      ABSTEN 
0.014935053 0.007018649 0.404420394 

Analyse des profils-lignes

regionalesCA$row

$coord
           Dim 1        Dim 2        Dim 3         Dim 4        Dim 5
PARI -0.10498220  0.002720771 -0.101621294 -0.0106552170 -0.006805277
SMAR  0.08205669 -0.118055641  0.033233371 -0.0231068110  0.007661099
YVEL -0.09597746 -0.039670407  0.055520970 -0.0029318843 -0.001521954
ESSO  0.01826232 -0.039252973 -0.035484742  0.0441840677  0.014858523
HTSS -0.15856949  0.082371853  0.075166586  0.0041979672 -0.001051224
STDE  0.24784182  0.095411070  0.001689557 -0.0005597677 -0.009628413
VDMA  0.07059721  0.066742451 -0.011532432 -0.0150918930  0.020815947
VDOI  0.08536010 -0.051274382  0.020568553  0.0134240837 -0.023053851

$contrib
          Dim 1       Dim 2        Dim 3        Dim 4       Dim 5
PARI 13.3673508  0.02916064 55.609197887  5.964688733  5.59549993
SMAR  5.2798720 35.49506407  3.845097457 18.135293778  4.58469895
YVEL  8.3039538  4.60764306 12.337401443  0.335652022  0.20800941
ESSO  0.2461197  3.69299462  4.125541631 62.404377816 16.23001984
HTSS 22.4468850 19.67313297 22.393892855  0.681465766  0.09827452
STDE 41.8441416 20.14104834  0.008633644  0.009245923  6.29112194
VDMA  3.6893243 10.70964726  0.437095902  7.303119213 31.95195285
VDOI  4.8223529  5.65130905  1.243139182  5.166156749 35.04042257

$cos2
          Dim 1        Dim 2        Dim 3        Dim 4        Dim 5
PARI 0.51216943 0.0003440063 4.799011e-01 5.276026e-03 2.152157e-03
SMAR 0.29925815 0.6194289520 4.908703e-02 2.373002e-02 2.608556e-03
YVEL 0.65169268 0.1113365305 2.180813e-01 6.081322e-04 1.638731e-04
ESSO 0.06273882 0.2898475174 2.368688e-01 3.672450e-01 4.153132e-02
HTSS 0.66678978 0.1799315491 1.498302e-01 4.673344e-04 2.930492e-05
STDE 0.86906696 0.1287957663 4.038774e-05 4.433224e-06 1.311636e-03
VDMA 0.48032922 0.4293073139 1.281757e-02 2.195085e-02 4.175960e-02
VDOI 0.65290081 0.2355798901 3.790922e-02 1.614755e-02 4.762383e-02

$inertia
[1] 0.0039470206 0.0026681799 0.0019269914 0.0005932636 0.0050910205
[6] 0.0072814710 0.0011615704 0.0011169905

Analyse des profils-colonnes

regionalesCA$col

$coord
              Dim 1        Dim 2        Dim 3        Dim 4        Dim 5
HUCHON  -0.04214027 -0.016535313 -0.102396641  0.015721728  0.002368643
COPE    -0.13049978 -0.051259901  0.008879053 -0.032486081  0.010821521
SANTINI -0.23884829  0.095483559  0.082164165  0.022472233 -0.003454881
LEPEN    0.16280744 -0.114613034  0.088268958  0.017436021  0.001675579
BUFFET   0.25807846  0.225925318 -0.011737861 -0.017830144  0.025942898
LAGU     0.16554084 -0.008410599  0.006615745  0.021228706 -0.002023908
PELEG    0.03316719 -0.071358579  0.062486721  0.049921119  0.060126767
BAY      0.15137821 -0.119841097  0.121097705  0.016027486  0.035025115
ABSTEN   0.05383430  0.005755252  0.005947334 -0.005495228 -0.010009797

$contrib
             Dim 1       Dim 2       Dim 3      Dim 4       Dim 5
HUCHON   2.2344494  1.11737699 58.57474413 13.4717980  0.70324745
COPE    16.6285871  8.33278923  0.34176866 44.6354179 11.39057588
SANTINI 36.2177096 18.79892256 19.02850838 13.8873155  0.75487683
LEPEN   12.7942164 20.59360077 16.69722716  6.3563692  0.13499836
BUFFET  18.8972892 47.03540331  0.17355499  3.9071032 19.02243958
LAGU     4.3053856  0.03609563  0.03052969  3.0668880  0.06410865
PELEG    0.1086391  1.63327947  1.71201547 10.6607275 35.56624355
BAY      1.0635124  2.16484310  3.02169614  0.5164113  5.67163393
ABSTEN   7.7502112  0.28768894  0.41995538  3.4979693 26.69187576

$cos2
            Dim 1       Dim 2       Dim 3       Dim 4        Dim 5
HUCHON  0.1387783 0.021367394 0.819404108 0.019316449 4.384558e-04
COPE    0.8138642 0.125570588 0.003767608 0.050434421 5.596404e-03
SANTINI 0.7767555 0.124135860 0.091918928 0.006875947 1.625198e-04
LEPEN   0.5538943 0.274502601 0.162815010 0.006352917 5.866897e-05
BUFFET  0.5604991 0.429537608 0.001159443 0.002675353 5.663806e-03
LAGU    0.9361807 0.002416591 0.001495226 0.015395592 1.399365e-04
PELEG   0.0603966 0.279568109 0.214373313 0.136824501 1.984865e-01
BAY     0.4189633 0.262579525 0.268115011 0.004696563 2.242892e-02
ABSTEN  0.9250910 0.010572922 0.011290441 0.009639129 3.198282e-02

$inertia
[1] 0.0024349319 0.0030898764 0.0070513836 0.0034932081 0.0050987336
[6] 0.0006954887 0.0002720267 0.0003838877 0.0012669713

Représentation des profils

plot.CA(regionalesCA, axes=c(1,2))

3.5 Exercices

Exercise 3.4 (TP avec prince sous Python) Le tableau \(10\times 8\) ci-dessous croise \(K=10\) catégories socioprofessionnelles avec \(L=8\) modes d’hébergements en vacances. Notons \(X\) et \(Y\) les variables en question.

X vs Y	hotel	locat	propri	parent	amis	tente	villag	divers	Total
Agriculteur	160	28	0	321	36	141	45	65	796
Salariés	35	34	1	178	8	0	4	0	260
Patrons	700	354	229	959	185	292	119	140	2978
Cadre sup	961	471	633	1580	305	360	162	148	4620
Cadre moy	572	537	279	1689	206	748	155	112	4298
Employés	441	404	166	1079	178	434	178	92	2972
Ouvriers	783	1114	387	4052	497	1464	525	387	9209
Personnels	65	43	21	294	79	57	18	6	580
Autres actif	77	189	189	839	53	124	28	53	1423
Non actifs	741	332	327	1789	311	236	102	102	3940
Total	4535	3377	2232	12780	1858	3856	1336	1105	31079

1. Déterminer le tableau des effectifs théoriques en cas d’indépendance.

2. Calculer la divergence du \(\chi^2\) entre le tableau réel et le tableau en cas d’indépendance.

3. Effectuer le test d’indépendance du \(\chi^2\).

4. Calculer la matrice \(X\) des profils-ligne et la matrice \(Y\) des profils-colonne. Discuter ces matrices.

5. On effectue une AFC à l’aide de la librairie prince de Python.

Exercise 3.5 (TP) We will use the MASS library for this assignment. Install and load it using:

library(MASS)

The following R commands are used to perform the analysis:

help(caith) # for function details
tab<-caith() # to create a variable containing the domain data
mosaicplot(tab) # to display the representation of row and column structure
chisq.test(tab) # to perform the chi-squared test
acf<-corresp(tab, nf=2) # to perform the correspondence analysis with two dimensions
plot(acf) # to display the first two components of the analysis

Exercise 3.6 Discussion about the distribution of \(n=10,000\) students in terms of their type of studies and the socio-professional category of their parents.

Category	Expl. Agricole	Expl. Agro	Salariat	Patron	Liberal	Cadre Moyen	Employe	Ouvrier	Service	Autres
Secondaire Non Diploma	60	36	132	19	65	23	11	54	58	42
Baccalaureat	8	72	315	67	64	58	21	48	62	90
Diplome Superieur	56	34	194	96	205	120	1	1	29	7
Pluridisc, IUT	476	191	896	400	876	564	465	79	57	35
Autres	305	115	624	217	301	47	42	90	90	90

library(FactoMineR)

# Create a data.frame df with these data
ca_results <- CA(df, graph = FALSE)
summary(ca_results)
plot(ca_results)

Exercise 3.7 Le tableau suivant représente le type d’études poursuivies (université, classes préparatoires, autres) en fonction du parcours suivi au lycée (Nomenclature des années 1970: A - Littéraire, B - Economie, C - Sciences (maths, physique), D - Sciences naturelles (biologie, chimie, …), E - Technologique “théorique”, Techn. - Technologique “appliqué”)

	Univ	Classes prépa	Autres
A	13	2	5
BDD’	20	2	8
CE	10	5	5
Techn.	7	1	22

1. Déterminer le tableau des effectifs théoriques sous l’hypothèse d’indépendance.

2. Calculer la distance du \(\chi^2\) entre le tableau réel et le tableau en cas d’indépendance.

3. Effectuer le test d’indépendance du \(\chi^2\) au niveau \(\alpha=10\%\).

4. Calculer la matrice \(T_r\) des profils-ligne et la matrice \(T_c\) des profils-colonne. Discuter ces matrices.

5. Quelles est la matrice sur laquelle repose la décomposition spectrale pour l’ACP des profils-lignes?

6. On effectue une AFC. Les valeurs propres différentes de 1 de \(S^2 = {}^tT_r{}T_c\) sont les suivantes:

\[ \text{Eigen values} : 0.1998 \quad 0.04936 \]

Interpréter ce résultat.

import pandas as pd

1df = pd.DataFrame({"Univ": [13, 20, 10, 7], "ClassesPrepa": [2, 2, 5, 1], "Autres": [5, 8, 5, 22]}, index=["A", "BDD", "CE", "Techn"])
2df

1

Créer le deteframe (données)

2

Afficher le jeu de données

       Univ  ClassesPrepa  Autres
A        13             2       5
BDD      20             2       8
CE       10             5       5
Techn     7             1      22

1import prince
2import matplotlib.pyplot as plt

3afc = prince.CA(n_components=2)
4afc.fit(df)

5coordonneesX = afc.row_coordinates(df)
6coordonneesY = afc.column_coordinates(df)

# Nuages des variables
plt.figure(figsize=(7, 7))
plt.scatter(coordonneesX[0], coordonneesX[1], label="X")
for j in range(len(coordonneesX[0])):
  plt.text(x= coordonneesX[0][j], y=coordonneesX[1][j], s = coordonneesX.index[j])
plt.scatter(coordonneesY[0], coordonneesY[1], label="Y")
for j in range(len(coordonneesY[0])):
  plt.text(x= coordonneesY[0][j], y=coordonneesY[1][j], s = coordonneesY.index[j])
plt.legend(loc="best")
plt.show()

1

Charger la librairie prince

2

Charger matplotlib.pyplot pour les graphiques

3

Instancier la class CA (Correspondances Analysis) de la librairie prince, pour \(2\) composantes

4

Ajuster le modèle

5

Coordonnées des modalités de \(X\) dans le plan

6

Coordonnées des modalités de \(Y\) dans le plan

<prince.ca.CA object at 0x746bffc42270>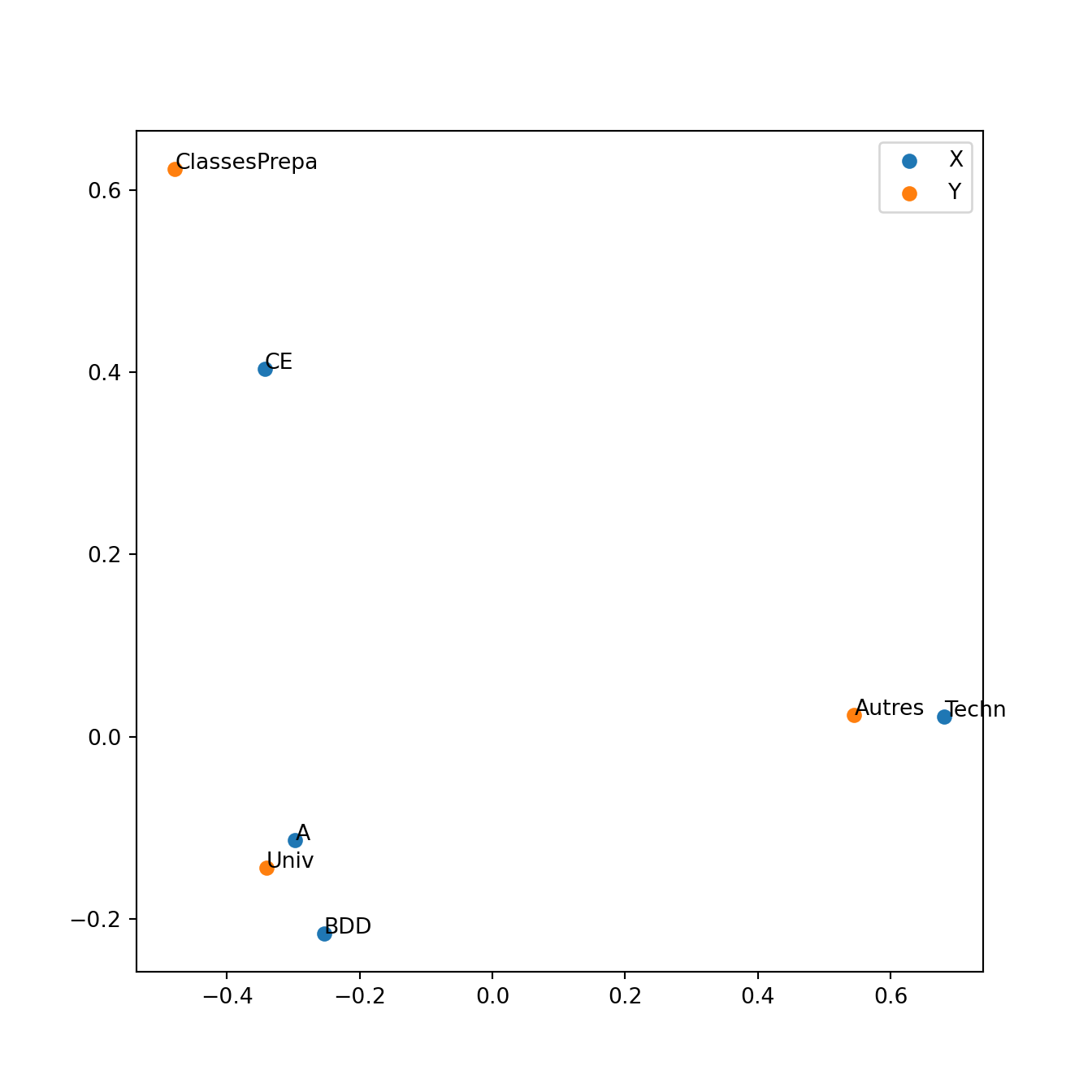

Exercise 3.8 Dans une entreprise, la répartition par sexe et par niveau d’emploi est la suivante :

	Ouvriers	Techniciens	Cadres
Hommes	20	40	40
Femmes	30	60	10

1. Y a-t-il un lien entre la répartition hommes-femmes et le niveau d’emplois? Confirmer ce résultat par un test du Khi-deux.

2. Réaliser une analyse factorielle des correspondances simples de ce tableau. On fournira la représentation simultanée des deux groupes de modalités.