2  Analyse en Composantes Principales

require(dplyr)
require(ggplot2)
require(reticulate)

Introduction

L’Analyse en Composantes Principales (ACP) est une technique statistique puissante utilisée pour réduire les dimensions de représentation des données, tout en conservant au mieux l’information qu’elles contiennent. C’est un outil essentiel dans la boîte à outils du data scientist, permettant de simplifier la complexité des données multidimensionnelles pour faciliter leur analyse et leur visualisation.

2.0.1 Mise en Contexte du Problème

Dans de nombreux domaines tels que la finance, la biologie, et le marketing, les professionnels sont confrontés à des ensembles de données de grandes dimensions. Ces ensembles peuvent contenir des centaines, voire des milliers de variables, rendant leur analyse ou leur visualisation très complexes, coûteuses en temps et en ressources, et souvent sujette à des interprétations erronées.

2.0.2 Objectifs du Chapitre

Ce chapitre vise à :

1. Expliquer les Principes Fondamentaux de l’ACP :

   • Introduction aux concepts mathématiques sous-jacents de l’ACP, y compris la covariance, les valeurs propres, et les vecteurs propres.

   • Compréhension de comment et pourquoi l’ACP est utilisée pour réduire la dimensionnalité des données.

2. Illustrer la Mise en Œuvre de l’ACP en R ou Python :
   • Démonstration pas à pas de la façon d’effectuer une ACP en utilisant le langage de programmation R, y compris la préparation des données, le calcul de l’ACP, et l’interprétation des résultats.
   • Exploration des différentes façons de visualiser les résultats de l’ACP pour une meilleure compréhension des structures cachées dans les données.
3. Discuter des Applications et des Considérations Pratiques :
   • Exemples d’applications de l’ACP dans divers domaines.
   • Discussion des avantages et des limites de l’ACP, ainsi que des considérations pratiques lors de son application à des ensembles de données réels.

En fournissant une compréhension approfondie de l’ACP, ce chapitre équipera les lecteurs avec les connaissances et les compétences nécessaires pour appliquer efficacement cette technique à leurs propres ensembles de données, leur permettant ainsi de révéler des insights précieux et de faciliter la prise de décision basée sur les données.

2.1 Formalisation du problème

On dispose de données sur \(n\) individus, décrites par \(p\) variables quantitatives \(X^1, X^2, ..., X^p\) présentant des liaisons multiples que l’on veut analyser. Ces observations sont regroupées dans une matrice \(X\in\mathbb{R}^{n\times p}\):

\[ X = \begin{bmatrix} x^1_1 & x^2_1 & \cdots & x^p_1 \\ x^1_2 & x^2_2 & \cdots & x^p_2 \\ \vdots & \vdots & \ddots & \vdots \\ x^1_n & x^2_n & \cdots & x^p_n \\ \end{bmatrix} \]

où \(x^j_i\) est la valeur observée de la \(j\)-ième variable \(X^j\) sur le \(i\)-ème individu de l’échantillon.

Example 2.1 (Decathlon)  

decathlon = read.csv("../../data/decathlon.csv", sep = ";")[, -1]
decathlon |>
  head(n = 5)

Les données précédentes sont les \(5\) premières lignes d’un jeu données présentant les résultats d’athlètes (individus) aux \(10\) épreuves (variables) d’un décathlon (Paris Rennes). On souhaite:

• Analyser les liaisons entre les performances aux différentes épreuves

• Savoir si certaines épreuves se ressemblent (une bonne performance à telle épreuve augure-t-elle une bonne performance à telle autre)

• Déterminer des profils d’athlètes (endurant, rapide, etc.).

Ainsi, sur les 10 épreuves, on se doute bien que les performances au 100m, 110m haies, et saut en longueur vont être corrélées.

Autres questions:

• Est-il vraiment utile de garder dans le tableau de données ces trois épreuves ?

• Ne peut-on pas se contenter d’en garder une seule ? Ou d’en “fabriquer” une qui serait un “résumé” de ces trois épreuves ?

• De façon générale, ne peut-on pas réduire la dimension du tableau de données, en ne conservant qu’un petit nombre de variables qui apportent autant d’information que l’ensemble des variables mesurées ?

Le but de l’ACP est de répondre à ce genre de questions. Son objectif principal est de remplacer la matrice \(X\) des données par une autre \(C_q\) de dimension réduite \((n, q)\) avec \(q \leq p\). Un des avantages de cette réduction de dimension est par exemple, de pouvoir obtenir des représentations graphiques des données.

En effet, lorsque \(p = 2\), chaque individu peut-être représenté par un point dans un plan, et le tableau de données peut être représenté graphiquement par un nuage de points dans un plan. Dès que \(p > 4\), une représentation graphique de même nature est difficile, et l’un des buts de l’ACP est de trouver “la meilleure” représentation plane possible des données initiales.

Avant de décrire plus précisément la méthode, il faut souligner quelques limites :

1. L’ACP ne permet pas le traitement de variables qualitatives;

2. L’ACP ne détecte que d’éventuelles liaisons linéaires entre variables.

L’ACP présente de nombreuses variantes selon les transformations apportées au tableau de données. Parmi ces variantes, l’ACP sur un tableau où les colonnes sont centrées et réduites, appelée ACP normée est la plus fréquemment utilisée.

2.2 Espace des individus - Espace des variables

2.2.1 Espace des individus.

On associe à chaque individu \(i\), un vecteur \(x_i\):

\[ x_i' = \left(x_i^{1}, x_i^{2}, ..., x_i^{p}\right)\in\mathbb{R}^p, \] la \(i\)-ème ligne de la matrice \(X\).

Chaque individu peut alors être représenté par un point dans \(\mathbb{R}^p\), appelé espace des individus.

2.2.1.1 Matrice des poids.

On affecte à chaque individu un poids \(p_i\) reflétant son importance par rapport aux autres individus avec \(p_i > 0\) et \(\sum_{i=1}^n p_i = 1\). On appelle matrice des poids la matrice diagonale \((n, n)\) dont les éléments diagonaux sont les poids \(p_i\). Elle sera notée

\[ D = \text{diag}(p_1, p_2, ..., p_n) = \begin{pmatrix} p_1 & 0 & \cdots & 0 \\ 0 & p_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & p_n \end{pmatrix} \]

Le cas le plus fréquent est de considérer que tous les individus ont la même importance : \(p_i = \dfrac{1}{n}\), pour tout \(i = 1, ..., n\). Si les individus sont par exemple des pays, on peut être amené à prendre

\[ p_i = \frac{\text{Population du pays } i}{\text{Population totale}}. \]

On appelle nuage des individus, l’ensemble des points \(x_i\) munis de leurs poids : \(\mathcal{M} = \{(x_i, p_i); i = 1, ..., n\}\).

2.2.1.2 Centrage des données.

Definition 2.1 (Centre de gravité) On appelle ainsi le point \[ g=\left(\bar{x}^j\right)_{j=1}^p\in\mathbb{R}^p, \] où \(\bar{x}^j=\sum_{i=1}^np_ix_i\) est la moyenne pondérée de le colonne \(j\) de \(X\).

Pn remarque que:

\[ g = {}^tXD \mathbf{1}_n, \]

où \(\mathbf{1}_n=\left(1\right)_{i=1}^n\in\mathbb{R}^n\) désigne le vecteur de \(\mathbb{R}^n\) dont toutes les coordonnées sont égales à \(1\).

Pour ramener l’origine du repère au barycentre (i.e. centrer le nuage autour de son barycentre), on centre les variables. À chaque variable observée \(x_i^j\), on associe sa variable centrée \(y_i^j\) :

\[ y^j = x^j - \bar{x}^j \mathbf{1}. \]

Definition 2.2 (Données centrées) \[ Y = \begin{bmatrix} y_1^1 & \cdots & y_1^p \\ y_2^1 & \cdots & y_2^p \\ \vdots & & \vdots \\ y_n^1 & \cdots & y_n^p \end{bmatrix} = \begin{bmatrix} y_1' \\ y_2' \\ \vdots \\ y_n' \end{bmatrix}, \]

avec \(y_i^j = x_i^j - \bar{x}^j\).

En utilisant les notations matricielles, on a

\[ Y = X - \mathbf{1}_n{}^tg. \]

2.2.1.3 Matrice des covariances empiriques

La matrice de covariance empirique des variables \(x^1, ..., x^p\) peut s’écrire sous la forme

\[ S^2 = X'DX - gg' = Y'DY=:\left(S_{j,k}\right)_{j,k}, \] avec \[ S_{j,k}={}^ty^jDy^{k} \] la covariance entre \(x^j\) et \(x^k\).

La variance de la variable \(x^j\) est:

\[ S_j^2:=S_{j,j} := \sum_{i=1}^{n} p_i (y_i^j)^2={}^ty^jDy^j, \]

Note

\(S^2\) est une matrice carrée \(p \times p\) symétrique semi-définie positive comme toute matrice de variances-covariances. Elle admet donc \(p\) valeurs propres réelles positives ou nulles.

2.2.1.4 Données centrées et réduites

Notons \(S_j:=\sqrt{S_j^2}\) l’écart-type empirique de la variable \(x^j\).

Les données centrées réduites sont alors données par la matrice

\[ Z = \begin{pmatrix} z_1^1 & \cdots & z_1^p \\ \vdots & & \vdots \\ z_n^1 & \cdots & z_n^p \end{pmatrix}, \]

où

\[ z_i^j = \dfrac{y_i^j}{S_j}=\dfrac{x_i^j-\bar{x}^j}{S_j}. \]

Si on note \(D_{S}\) la matrice diagonale des inverses des écarts-types :

\[ D_S = \text{diag}\left(\frac{1}{S_1}, \ldots, \frac{1}{S_p}\right) = \begin{pmatrix} \frac{1}{S_1} & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \frac{1}{S_p} \end{pmatrix}, \]

le tableau \(Z\) peut être écrit sous la forme \[Z = YD_S.\]

2.2.1.5 Matrice de corrélations empiriques

Notons \(R\), la matrice empirique des corrélations des variables \(x^1, \ldots, x^p\) : \[ r_{jk} = \text{cor}(x^j, x^k). \]

La matrice \(R\) de corrélation empirique

\[ R = \begin{pmatrix} 1 & r_{12} & \cdots & r_{1p} \\ r_{21} & 1 & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & 1 \end{pmatrix}, \]

peut se définir

\[ R = {}^tZ DZ. \]

Note

La matrice des corrélation des données \(X\) est celle es variances-covariances des données centrés-réduites \(Z\).

2.2.1.6 Espace métrique des individus

Si l’on veut faire des “groupes d’individus qui se ressemblent” au vu des variables considérées, il faut introduire une mesure de “proximité” entre individus, i.e. définir une notion de distance sur l’espace vectoriel des individus. Quelle distance choisir ? La question est primordiale car les résultats de l’étude statistique vont en dépendre dans une large mesure.

On pourrait choisir la distance euclidienne usuelle

\[ d(x_1, x_2) = \sqrt{\sum_{j=1}^p(x_1^j - x_2^j)^2}, \]

mais ce n’est pas forcément la plus adaptée. Par exemple, on peut vouloir donner des importances différentes à chaque variable, auquel cas on choisira plutôt de prendre pour distance

\[ d(x_1, x_2) = \sqrt{\sum_{j=1}^pm_j(x_1^j - x_2^j)^2}. \]

Cela revient à multiplier par \(\sqrt{m_j}\) chaque variable \(X_j\). Cependant, cette formule sous-entend que les axes sont orthogonaux (formule de Pythagore), mais en statistique c’est par pure convention que l’on représente les variables sur des axes orthogonaux, on aurait pu prendre des axes obliques. Ainsi, la distance entre deux individus \(x_1\) et \(x_2\) peut être définie de manière générale par :

\[ d_M(x_1, x_2) = \sqrt{(x_1 - x_2)'M(x_1 - x_2)} =: \|x_1 - x_2\|_M , \]

où \(M\) est une matrice symétrique définie positive : pour tout \(u \in \mathbb{R}^p\), \(u'Mu \geq 0\) et si \(u'Mu = 0\) alors \(u = 0_p\). Une telle matrice admet \(p\) valeurs propres réelles strictement positives.

En pratique, on utilise le plus souvent l’une des métriques suivantes :

• \(M = I_p\): La distance associée est la distance euclidienne usuelle, et on parle d’ACP canonique ou simple. Elle s’utilise lorsque les variable sont homogènes (même dimension) et de même ordre de grandeur;

• \(M = D_{S^2}:= diag\left(\frac{1}{S_1^2}\cdots,\frac{1}{S_p^2}\right)\): Le choix de cette métrique revient à utiliser la métrique usuelle précédante sur les données centrées et réduites \(Z\). Son rôle est d’équilibrer les dispersion des variables.

2.2.2 Espace métrique des variables

De la même façon que ce qui a été fait pour un individu, on peut associer à chaque variable \(X^j\) le vecteur \(x^j\) contenant les valeurs prises par cette variable sur l’ensemble des \(n\) individus :

\[ x^j = \begin{pmatrix} x_1^j \\ x_2^j \\ \vdots \\ x_n^j \end{pmatrix} = \mathbb{R}^n\equiv \text{j-ième colonne de X}. \]

Chaque variable \(X^j\) peut alors être représentée par un vecteur de \(\mathbb{R}^n\) appelé espace vectoriel des variables.

Si on veut juger de la “proximité” entre deux variables, il faut encore une fois munir \(\mathbb{R}^n\) d’une distance qui rend compte de cette proximité, i.e. choisir une matrice \(M\) (\(n, n\)) symétrique et définie positive. Ici, un choix naturel consiste à prendre \(M = D\), la matrice diagonale des poids (dite métrique des poids). En effet, si \(y^1, y^2, \ldots, y^p\) sont les variables centrées associées à \(x^1, x^2, \ldots, x^p\), on a

\[ \langle y^j, y^k \rangle_D = \sum_{i=1}^n p_i y_i^j y_i^k = \text{cov}(x^j, x^k); \]

\[ \| y^j \|_D^2 = s_j^2. \]

De plus l’angle \(\theta_{jk}\) entre les vecteurs \(y^j\) et \(y^k\) est donné par

\[ \cos(\theta_{jk}) = \frac{\langle y^j, y^k \rangle_D}{\| y^j \|_D \| y^k \|_D} = \frac{\text{cov}(x^j, x^k)}{s_j s_k} = r_{jk}. \]

En résumé, lorsque les variables sont centrées et représentées par des vecteurs de \(\mathbb{R}^n\) muni de la métrique des poids :

• la longueur du vecteur correspond à l’écart-type de la variable associée,
• le cosinus de l’angle de deux vecteurs représente la corrélation linéaire des deux variables associées.

2.3 Inertie d’un nuage de points.

Soit \(M = \{(x_i, p_i)\}\) le nuage de points. On note \(\mathcal{N} = \{(\nu_i, p_i)\}\) le nuage centré, où on a ramené le centre de gravité à l’origine du repère.

2.3.1 Inertie totale du nuage de points.

Notons:

• \(\langle u, v\rangle_{M}:={}^tuMv\) le produit scalaire défini par \(M\)

• \(\|u\|_M=\sqrt{\langle u,u\rangle_M}\) la norme associée.

Definition 2.3 (Inertie totale) On appelle inertie totale du nuage des individus, \(I\), la moyenne pondérée des carrés des distances des points au centre de gravité :

\[ I = \sum_{i=1}^n p_i d_M^2(x_i, g) = \sum_{i=1}^n p_i\|x_i - g\|^2_M = \sum_{i=1}^n p_i\|y_i\|^2_M. \]

Note

• L’inertie mesure la dispersion des points individus autour du centre de gravité \(g\), elle est parfois appelée variance du nuage.

• L’inertie du nuage \(\mathcal{M}\) est évidemment égale à l’inertie du nuage centré \(\mathcal{N}\).

• L’inertie est aussi une mesure de l’information du nuage des individus.

Proposition 2.1 \[ I = \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n p_ip_j\|x_i - x_j\|^2_M, \]

c’est à dire l’inertie correspond à la moyenne des carrés de toutes les distances entre les individus.

Proof 2.6. Notons \((x, y)\) le produit scalaire associé à \(M\) : \((x, y) = x'My\).

\[ \begin{align*} I &= \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n p_ip_j\|x_i - x_j\|^2_M \\ &= \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n p_ip_j\|x_i - g + g - x_j\|^2_M \\ &= \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \left( p_ip_j\|x_i - g\|^2_M + p_ip_j\|x_j - g\|^2_M - 2p_ip_j(x_i - g, x_j - g)_M \right) \\ &= \sum_{i=1}^n p_i\|x_i - g\|^2_M, \end{align*} \]

puisque \(\sum_{i=1}^n p_i(x_i - g) = 0\) par définition de \(g\).

2.3.2 Inertie expliquée par un sous espace \(F\).

Definition 2.4 (Inertie expliquée) On appelle \(inertie du nuage\) des individus \(\mathcal{N}\) expliquée (portée) par le sous-espace vectoriel \(F\) de \(\mathbb{R}^p\), l’inertie du nuage projeté \(M\)-orthogonalement sur \(F\), c’est-à-dire :

\[ I_F(\mathcal{N}) =\sum_{i=1}^n p_i\|y_i^F\|^2_M , \]

où \(y_i^F\) désigne la projection \(M\)-orthogonale de \(y_i\) sur \(F\). Autrement dit,

\[ I_F(\mathcal{N}) = I(\mathcal{N}^F) , \]

où \(\mathcal{N}^F = \{(y_i^F, p_i)\}\) est le projeté du nuage centré.

Par exemple, si \(u\) est un vecteur \(M\)-normé (i.e. \(\|u\|_M^2 = 1\)), et \(\Delta_u\), est la droite vectorielle engendrée par \(u\), la projection orthogonale de \(y_i\) sur \(\Delta_u\) est \[ y_i^u= \langle y_i, u\rangle_M\cdot u={}^ty_iMu, \] et l’inertie expliquée par \(\Delta_u\) est donnée par

\[ \begin{align*} I_{\Delta_u} &= I(\mathcal{N}^u) = \sum_{i=1}^n p_i\|y_i^u\|^2_M \\ &= \sum_{i=1}^n p_i({}^ty_i^uM y_i^u) \\ &= {}^tuM \left(\sum_{i=1}^n p_i y_i y_i'\right) Mu \\ &= {}^tu M S^2 Mu.\\ \end{align*} \]

Proposition 2.2 (Décomposition de l’inertie)  

1. Si \(F\) est un s.e.v. de \(\mathbb{R}^p\) et si \(F^\perp\) désigne son supplémentaire \(M\)-orthogonal, on a la décomposition suivante :

\[ I = I_F + I_{F^\perp} . \]

2. De façon plus générale, si \(F = F_1 \oplus F_2\) et \(F_1 \perp F_2\) (au sens du produit scalaire défini par M), alors

\[ I_F = I_{F1} + I_{F2} . \]

La quantité \(I_{F^\perp}\) peut donc être considérée comme une mesure de la déformation du nuage lors de la projection sur \(F\) :

\[ I_{F^\perp} = \sum_{i=1}^n p_i\|y_i^{F^{\perp}}\|^2_M . \]

Pour tout s.e.v. F de \(\mathbb{R}^p\), l’inertie totale se décompose comme la somme de

• L’inertie totale du nuage projeté sur \(F\) (\(I(\mathcal{N}^F)\)),
• La déformation du nuage \(\mathcal{N}\) par projection orthogonale sur \(F\).

Proof 2.6.

1. Tout élément de \(\mathbb{R}^p\) se décompose de manière unique sous la forme

\[ x = x^F + x^{F^\perp}, \quad x^F \in F, x^{F^\perp} \in F^\perp, \quad \langle x^F; x^{F^\perp}\rangle_M = 0 . \]

Par conséquent,

\[ \begin{align*} I &= \sum_{i=1}^n p_i\|y_i\|^2_M = \sum_{i=1}^n p_i\|y_i^F + y_i^{F^\perp}\|^2_M\\ &= \sum_{i=1}^n p_i\|y_i^F\|^2_M + \sum_{i=1}^n p_i\|y_i^{F^\perp}\|^2_M + 2 \sum_{i=1}^n p_i\langle y_i^F; y_i^{F^\perp}\rangle_M\\ &= I_F + I_{F^\perp}.\\ \end{align*} \]

2. De la même façon, tout élément de \(F\) se décompose de manière unique sous la forme

\[ x = x^{F1} + x^{F2}, \quad x^{F1} \in F_1, x^{F2} \in F_2, \quad \langle x^{F1}; x^{F2}\rangle_M = 0 . \]

On a donc \(y_i^F = (y_i^F)^{F1} + (y_i^F)^{F2}\). Comme \(F_1 \perp F_2\), \((y_i^F)^{F1} = y_i^{F1}\). De même, \((y_i^F)^{F2} = y_i^{F2}\).

Par conséquent,

\[ \begin{align*} I_F &= \sum_{i=1}^n p_i\|y_i^F\|^2_M \\ &= \sum_{i=1}^n p_i\|y_i^{F1}\|^2_M + \sum_{i=1}^n p_i\|y_i^{F2}\|^2_M\\ &= \sum_{i=1}^n p_i\|y_i^{F1}\|^2_M + \sum_{i=1}^n p_i\|y_i^{F2}\|^2_M + 2 \sum_{i=1}^n p_i(y_i^{F1}; y_i^{F2})_M\\ &= I_{F1} + I_{F2} . \end{align*} \]

2.4 Principes de l’ACP des individus

2.4.1 Rappel du problème.

Rappelons que l’objectif principal est de réduire la dimension de représentation du nuage des individus en concervant au mieux l’information (inertie). Autrement dit, on cherche le sous-espace \(E_q\) de dimension \(q\leq p\) portant l’inertie maximale du nuage:

\[ \max_{dim E=q}I_E \tag{2.1}\]

Definition 2.5 (Sous-espace principal) On appelle sous-espace principal de dimension \(q\), tout sous-espace vectoriel de dimension \(q\) solution du problème d’optimisation Equation 2.1.

2.4.2 Espaces et axes principaux.

Theorem 2.1 Soit \(E_q\) un sous espace vectoriel de dimension \(q < p\) portant l’inertie maximale du nuage, alors un sous-espace de dimension \(q + 1\) portant l’inertie maximale est

\[ E_{q+1} = E_q \oplus \Delta_{u_{q+1}} \]

où

• \(u_{q+1}\) est un vecteur \(M\)-orthogonal à \(E_q\) et

• \(\Delta_{u_{q+1}}\) est une droite vectorielle \(M\)-orthogonale à \(E_q\) portant l’inertie maximale parmi toutes les droites vectorielles M-orthogonales à \(E_q\).

Proof 2.6. Soit \(F\) un sous-espace de dimension \(q + 1\). Comme \(\dim(E_q') + \dim(F) = (p - q) + (q + 1) = p + 1\), \(E_q'\) et \(F\) ont au moins une direction commune. Soit \(u \in E_q' \cap F\) (u ≠ 0). On peut alors écrire \(F = F' \oplus \Delta_u\), où \(F'\) est le supplémentaire orthogonal de \(\Delta_u\), dans \(F\). \(F'\) est de dimension \(q\), et par définition de \(E_q\), on a donc \(I_F \leq I_{E_q}\). Par ailleurs, par définition de \(u_{q+1}\), on a aussi \(I_{E_q \oplus \Delta_u} = I_{E_{q+1}}\), donc

\[ I_F = I_{F'} + I_u \leq I_{E_q} + I_{u_{q+1}} = I_{E_{q+1}} \]

où \(E_{q+1} = E_q \oplus \Delta_{u_{q+1}}\).

Definition 2.6 (Axes principaux) Les axes \(\Delta_{u_1}, \ldots, \Delta_{u_p}\), sont appelés axes principaux d’inertie de l’ACP.

Note

Le Theorem 2.1 dit que les sous-espaces principaux \(E_q\) (les solutions de Equation 2.1) sont emboîtés et peuvent se calculer de façon itérative selon la procédure :

• Rechercher un axe \(\Delta_{u_1}\) maximisant l’inertie expliquée \(I_{\Delta_{u_1}}\). On note \(E_1 = \Delta_{u_1}\).

• Rechercher un axe \(\Delta_{u_2}\) orthogonal à \(E_1\), maximisant l’inertie expliquée \(I_{\Delta_{u_2}}\). On note \(E_2 = E_1 \oplus \Delta_{u_2}\).

• …

• Rechercher un axe \(\Delta_{u_q}\) orthogonal à \(E_{q-1}\) maximisant l’inertie expliquée \(I_{\Delta_{u_q}}\). On note \(E_q = E_{q-1} \oplus \Delta_{u_q}\).

2.4.3 Calcul des axes principaux

• Commenceons par trouver l’axe principal \(\Delta_{u_1}\), avec \(\|u_1\|_M^2\) est \(M\)-normé. Rappelons que l’inertie expliquée par \(\Delta_{u_1}\) est \[ I_{\Delta_{u_1}} = {}^tu_1MS^2Mu_1. \]

Le problème d’optimisation est alors \[ \max_{|\|u\|_M^2}{}^tuMS^2Mu. \tag{2.2}\]

• L’axe principal \(\Delta_{u_2}\) est la solution de \[ \max_{|\|u\|_M^2,\ {}^tuMu_1=0}{}^tuMS^2Mu. \]

Theorem 2.2 (Axes principaux) Supposons que \(rg(X)=p\).

1. Alors les \(p\) axes principaux \(\Delta_{u_k}\), \(k=1,\cdots,p\) sont donnés par les \(p\) vecteurs propres \(M\)-normés \(u_1,\cdots,u_p\), rangés selon l’ordre décroissant des \(p\) valeurs propres réelles \(\lambda_1>\cdots>\lambda_p>0\) de la matrice \(S^2M\);

2. L’espace principal \(E_q\) de dimension \(q\) est donné par \(E_q=Vect\left(u_1,\cdots,u_q\right)\), et l’inertie expliquée par \(E_q\) est donnée par \[I_{E_q} = \lambda_1 + \cdots + \lambda_q.\]

Proof 2.6 (En exercice).

Definition 2.7 (Vecteurs principaux) Les vecteurs \(u_j\) sont appelés vecteurs principaux de l’ACP.

Note

• Il est important de noter que par construction, les \(u_j\) sont \(M\)-orthonormés: \[ {}^tUMU=I. \]

2.4.4 Composantes Principales (CP)

Rappelons que le problème pour les individus était d’obtenir une représentation du nuage \(\mathcal{N}\) dans des espaces de dimensions réduites. On connait maintenant les axes définissant ces espaces. Pour pouvoir obtenir les différentes représentations, il suffit de déterminer les coordonnées des points du nuage projeté \(M\)-orthogonalement sur chaque axe principal. Soit \(c_1^j, c_2^j, \ldots, c_n^j\) les coordonnées sur l’axe \(\Delta_{u_j}\), où \(c_i^j\) est la coordonnée de \(y_i\) sur l’axe \(\Delta_{u_j}\).

\[ c_i^j = \langle y_i, u_j \rangle_M = {}^ty_iMu_j . \]

Definition 2.8 (Composante principale) Le vecteur de \(\mathbb{R}^n\)

\[ c^j = \begin{pmatrix} c_1^j \\ c_2^j \\ \vdots \\ c_n^j \end{pmatrix} = YMu_j . \]

est appelé \(j\)-ième composante principale.

Definition 2.9 (Matrice des composantes principales)  

• La matrice \(CP = [c^1, c^2, \ldots, c^p]\) dont les colonnes sont les composantes principales \(c^j\) est appelée matrice des composantes principales.

• En posant \(U = [u_1, u_2, \ldots, u_p]\), on a \[ C=YMU \]

Note

• Les coordonnées des individus de \(n\)-échantillon dans l’espace principal \(E_q\) sont données par les \(q\) premières collones \([C]_q=[c^1\cdots c^q]\) de \(C\).

Proposition 2.3  

1. Les CP sont des combinaisons linéaires des variables de départ dans les données centrées \(Y\): \[ c^j=Mu_j \]

2. Les CP sont centrées: \(\sum_{i=1}^np_ic_i^j=0\).

3. Les CP sont décorrelées et de variances les \(\lambda_j\): \({}^tCDC = \Lambda:=diag\left(\lambda_1,\cdots,\lambda_r\right)\)

4. Les \(c^j\) sont les vecteurs propres de \({}^tYM{}^tY\), de valeurs propres les \(\lambda_j\).

Proof 2.6 (En exercice).

Definition 2.10 (Facteurs principaux) On appelle ainsi les

\[ f^j = \frac{c^j}{\sqrt{\lambda_j}}\in\mathbb{R}^n. \]

Note

• Remarquer que les facteurs principaux sont données dans les colonnes de la matrice \[ F=C\Lambda^{-\frac{1}{2}} \]

• Les facteurs principaux sont \(D\)-orthonormés: \[ {}^tFDF=I. \]

• Il ne constituent pas nécessairement une base de \(\mathbb{R}^n\) (puisque \(r \leq \min(n,p)\)).

Note

Nous venons de décrire la solution du problème de réduction de la dimension de représentation des données: on peut alors parler de l’ACP\((Y, D, M)\) où rappelons le:

• \(D\) est la matrice des poids

• \(M\) est la métrique sur l’espace des individus qui sont les lignes de \(Y\).

2.5 ACP dans l’espace des variables.

Nous nous intéressons maintenant à la réduction de la dimension de représentation des variables \(y^j\in\mathbb{R}^n\).

Pour réduire la dimension de représentation du nuage des variables, on adopte la même démarche que pour le nuage des individus, en faisant l’\(ACP\left({}^tY, M, D\right)\). L’objectif est de trouver les sous-espaces principaux \(F_q\) qui conservent au mieux l’information liée à l’inertie contenue dans le nuage des variables. Pour construire cette ACP, on a besoin:

• Des données: \({}^tY\in\mathbb{R}^{p\times n}\);

• D’une matrice \((p, p)\) de poids: on va ici choisir la matrice \(M\);

• D’une métrique sur l’espace des variables \(\mathbb{R}^n\): on a déjà vu qu’un choix naturel est de prendre \(D = \text{diag}(p_1, \ldots, p_n)\).

Avec ce choix de métrique et de matrice de poids, on a le résultat :

Proposition 2.4  

1. Les ACP \(({}^tY, M, D)\) et \((Y, D, M)\) ont les mêmes valeurs propres non nulles \(\lambda_1> \ldots> \lambda_r>0\).

2. Les axes principaux de l’ACP\(({}^tY, M, D)\) correspondant aux valeurs propres non nulles \(\lambda_1> \ldots> \lambda_r\), sont les facteurs principaux \(F=[f^1\cdots f^r]=C\Lambda^{-\frac{1}{2}}\) de l’ACP\((Y, D, M)\) des individus.

3. Les composantes principales non nulles de l’ACP\(({}^tY, M, D)\) du nuage des variables sont les colonnes de la matrice \(U\Lambda^{\frac{1}{2}}=\left[\sqrt{\lambda_1}u_1 \cdots \sqrt{\lambda_r}u_r\right]\)

4. Les facteurs principaux de l’ACP\(({}^tY, M, D)\) du nuage des variables, sont les axes principaux \(U=\left[u_1 \cdots u_r\right]\) de l’ACP\((Y, D, M)\) du nuage des individus, correspondant aux valeurs propres non nulles.

Proof 2.6 (En exercice). On rappelle les résultats:

• Pour faire l’ACP\(({}^tY, M, D)\) du nuage des variables, il faut diagonaliser la matrice \((n, n)\) \(YM{}^tYD\).

• Soit \(A\) une matrice \((n, p)\) et \(B\) une matrice \((p, p)\) inversible. Alors \(\text{rang}(AB) = \text{rang}(A)\).

• Soit \(A\) une matrice \((n, p)\). Alors \(\text{rang}(A^tA) = \text{rang}(A^t) = \text{rang}(A)\).

2.6 Résumé d’une analyse en composantes principales.

Les sorties de l’ACP\((Y, D, M)\) sont :

• Matrice des variances-covariances: \(S^2={}^tYDY\)

• Décomposition spectrale de \(S^2M\):

  • Vecteurs propres \(M\)-othonormés \(U=[u_1\cdots u_r]\) rangés selon les

  • Valeurs propres \(\lambda_1>\cdots>\lambda_r>0\)

• Les axes principaux sont \(u_1, \ldots, u_r\);

• Les facteurs principaux sont les \(F=C\Lambda^{-\frac{1}{2}}\)

• Les composantes principales du nuages des individus \(C=YMU\in\mathbb{R}^{n\times r}\)

• Les composantes principales non-nulles du nuages des variables sont les colonnes de \(U\Lambda^{\frac{1}{2}}\)

	Individus	Variables
Espace vectoriel	\(\mathbb{R}^p\)	\(\mathbb{R}^n\)
Tableau des données	\(Y\in\mathbb{R}^{n\times p}\)	\({}^tY\in\mathbb{R}^{p\times n}\)
Matrice des poids	\(D = diag(p_1, \ldots, p_n)\)	\(M\)
Métrique	\(M\)	\(D\)
Matrice à diagonaliser	\(S^2M = {}^tYDYM\)	\(YM{}^tYD\)
Valeurs propres non nulles	\(\lambda_1 > \cdots > \lambda_r > 0\)	\(\lambda_1 > \cdots > \lambda_r > 0\)
Axes principaux	\(U=[u_1 \cdots u_r]\)	\(F=[f^1 \cdots, f^r]=C\Lambda^{-\frac{1}{2}}\)
	\(\begin{cases} S^2MU = U\Lambda \\ {}^tUMU=I \end{cases}\)	\(\begin{cases} YM{}^tYDF = F\Lambda \\ {}^tFDF=I \end{cases}\)
Composantes principales	\(C = YMU\)	\({}^tYDF=U\Lambda^{\frac{1}{2}}\)
	\({}^tCDC=\Lambda\)
Facteurs principaux	\(F=C\Lambda^{-\frac{1}{2}}\)	\(U\)
Qualité de l’espace princ.	\(\dfrac{\sum_{j=1}^q\lambda_j}{\sum_{j=1}^r\lambda_j}\)	\(\dfrac{\sum_{j=1}^q\lambda_j}{\sum_{j=1}^r\lambda_j}\)

2.7 Représentations graphiques.

2.7.1 Représentation des individus.

2.7.1.1 La carte des individus.

Les coordonnées des individus dans l’espace principal \(E_q\) sont données par les \(q\) premières colonnes de la matrice \(C\) des composantes principales.

2.7.1.2 Qualité de la représentation du nuage des individus.

Rappelons que l’inertie totale du nuage des individus vaut

\[ I = \sum_{i=1}^p \lambda_i = \text{tr}(S^2M) . \]

Definition 2.11 (Qualité globale de représentation) La qualité globale de la représentation du nuage des individus sur \(E_q\) engendré par \((u_1, \ldots, u_q)\) est mesurée par le pourcentage d’inertie expliquée par \(E_q\)

\[ \frac{I_{E_k}}{I} = \frac{\lambda_1 + \ldots + \lambda_q}{\sum_{i=1}^r \lambda_i} . \]

Plus cette qualité est proche de \(1\), plus le nuage de points initial est “concentré” autour de \(E_q\), et plus fidèle est son image projetée sur \(E_q\).

2.7.1.3 Qualité de la représentation d’un individu.

Parallèlement à cet indice de qualité globale, on peut définir, pour chaque individu, la qualité de sa représentation sur \(E_q\).

Definition 2.12 (Qualité de représentation d’un individu) La qualité de représentation de l’individu \(i\) sur l’espace principal \(E_q\) est mesurée par le cosinus carré de l’angle que fait \(y_i\) avec sa projection \(M\)orthogonale \(P_{E_q}y_i\) sur \(E_q\):

\[ \cos^2\left(\widehat{y_i, P_{E_q}y_i}\right) = \dfrac{\sum_{j=1}^q\left( c_i^j\right)^2}{\sum_{j=1}^p \left(c_i^j\right)^2} . \]

• Si \(\cos^2(\widehat{y_i, P_{E_q}y_i})\) est proche de \(1\), l’individu \(i\) appartient “presque” à \(E_q\), et il est donc bien représenté sur \(E_q\).

• Si \(\text{cos}^2(\widehat{y_i, P_{E_q}y_i})\) est proche de \(0\), l’individu \(i\) est mal représenté sur \(E_q\).

Ainsi, la qualité de représentation de l’individu \(i\) sur le premier plan principal \(E_2\) est mesurée par

\[ \text{cos}^2(\widehat{y_i, P_{E_2}y_i}) = \frac{(c_i^1)^2 + (c_i^2)^2}{\sum_{j=1}^p (c_i^j)^2} . \]

Remarque

Dans une carte des individus, on peut lire des conclusions sur les individus (regroupements, individus exceptionnels, etc…) que si ces individus sont bien représentés dans le plan principal considéré.

2.7.1.4 Représentation des individus suplémentaires

Soit \(x\in\mathbb{R}^p\) les données d’un nouvelle individu n’ayant pas participé à l’estimation de l’ACP. Les coordonnées de cette individu dans le plan principal \(E_q\) sont données par les \(q\) premières coordonnées de \[ {}^t(x-g)MU. \]

Note

• Les individus supplémentaire sont généralement des centres de gravité de groupes d’individus;

• Ils servent surtout à l’interprétation des resultats;

2.7.2 Représentation des variables.

2.7.2.1 La carte des variables.

Dans l’espace des variables, les axes principaux correspondant aux valeurs propres non nulles sont les facteurs principaux \(d^1, \ldots, d^r\). Une variable \(y^j\) est donc représentée par sa projection \(D\)-orthogonale sur l’espace principal \(F_q\) (où \(q = 2\) ou \(3\)) engendré par \(d^1, \ldots, d^q\). Ses coordonnées sont alors données par les \(q\) premières colonnes de la matrice \[ {}^tYDF={}^tYDC\Lambda^{-\frac{1}{2}} = U\Lambda^{\frac{1}{2}} \]

Note

• Remarquer que le coefficient \((j,k)\) de la matrice \({}^tYDC\Lambda^{-\frac{1}{2}}\) est la covariance entre la variable \(y^j\) et le facteur principal \(f^k\).

2.7.2.2 Qualité de la représentation du nuage des variables :

L’inertie totale du nuage \(\mathcal{V}\) des variables vaut

\[ \begin{aligned} I(\mathcal{V}) &= \text{tr}(YM{}^tYD) \\ &= \sum_{j=1}^r \lambda_j = I(\mathcal{N}) = I. \end{aligned} \]

La qualité globale de la représentation du nuage \(\mathcal{V}\) sur le \(s.e.p\) \(F_q\) est mesurée par

\[ \frac{\sum_{j=1}^q \lambda_j}{\sum_{j=1}^r \lambda_j}. \]

2.7.2.3 Qualité de la représentation d’une variable :

La qualité de la représentation de la variable \(y^j\) sur l’axe principal engendré par \(f^k\) est mesurée par :

\[ \begin{aligned} \cos^2(y^j, f^k) &= cor^2(y^j, f^k)\\ &=cor^2(y^j, c^k) \end{aligned} \]

où \(cor(y^j, f^k)\) est le coefficient de corrélation linéaire entre \(y^j\) et \(f^k\).

Remarque

Comme \(f^k = \dfrac{c^k}{\sqrt{\lambda_k}}\), la qualité de la représentation de la variable \(y^j\) sur l’axe principal engendré par \(f^k\) est aussi égale à \(cor^2(y^j, c^k)\).

2.7.2.4 Cas particulier d’une ACP normée: Cercle des corrélations.

On se place ici dans le cadre d’une ACP normée c’est-à-dire l’ACP\((Z, D, I)\). Alors les coordonnées des projectés \(D\)-orthogonaux des variables \(z^j\) sont données dans la matrice \[ {}^tZDF={}^tZDC\Lambda^{-\frac{1}{2}}. \]

On remarque que cette matrice est celle des corrélations entre les \(y^j\) et les \(c^k\). Les coordonnées des variables sur \(F_2=Vect\left\{f^1, f^2\right\}\) sont données par les \(2\) premières colonnes de la matrice \({}^tZDF\).

Interprétation

Les cartes des variables facilitent l’interprétation de la matrice des corrélations des variables. Si deux variables \(z^i\) et \(z^j\) sont bien représentées par leurs \(D\)-projections sur le plan considérés, alors :

• La proximité des projections \(z^j\) et \(z^k\) indique une forte corrélation linéaire positive entre les deux,

• Des points \(z^j\) et \(z^k\) diamétralement opposés indiquent une forte corrélation négative proche,

• Des directions de \(z^j\) et \(z^k\) presque orthogonales indiquent une faible corrélation entre les deux.

2.8 Reconstitution des données de départ.

À partir de la décomposition des vecteurs \(y_i\) de \(\mathbb{R}^p\) sur la base de vecteurs propres \(\{u_1, \ldots, u_p\}\)

\[ y_i = \sum_{j=1}^p c_i^j u_j = \sum_{j=1}^r \sqrt{\lambda_j} f_i^j u_j . \]

Proposition 2.5 (Formule de reconstitution) On en déduit la formule de reconstitution:

\[ Y =\sum_{j=1}^r \sqrt{\lambda_j} f^j u_j', \]

qui représente la matrice \(Y\) comme une somme de matrices de rang \(1\).

Cette relation montre que l’on peut “reconstituer” le tableau initial des données centrées à partir des valeurs propres \(\lambda_j\), des vecteurs principaux \(u_j \in \mathbb{R}^p\) et des facteurs principaux \(f^j \in \mathbb{R}^n\) associés, obtenus dans l’analyse des individus et des variables respectivement.

Si on se limite aux \(q\) (\(q < r\)) premiers termes, on obtient une approximation de rang \(q\) du tableau initial :

\[ Y \approx \widehat{Y} = \sum_{j=1}^q \sqrt{\lambda_j} f^j u_j' . \]

La matrice \(\widehat{Y}\) est de taille \((n, p)\), et de rang \(q\). En effet, pour tout \(j_0 \in \{1, \ldots, p\}\),

\[ \begin{aligned} \widehat{Y} M u_{j_0} &= \sum_{j=1}^q \langle f^j u_j', M u_{j_0} \rangle\\ &= \begin{cases} \sqrt{\lambda_{j_0}} f^{j_0} & \text{si } j_0 \leq q, \\ 0 & \text{si } j_0 > q. \end{cases} \\ \end{aligned} \]

On en déduit que \(\text{rg}(\widehat{Y}M) = q\), et comme \(M\) est inversible, il résulte que \(\text{rang}(\widehat{Y}) = q\).

Le théorème d’Eckart-Young établit que cette somme des \(q\) premiers termes de rang \(1\) fournit la meilleure approximation de \(Y\) par une matrice de rang \(q\) au sens des “moindres carrés” :

\[ \| Y - \widehat{Y} \|^2_{M,D} = \inf_{T\in\mathbb{R}^{n\times p},\ rg(T)=q} \| Y - T \|^2_{M,D}, \]

où on a noté \(\| T \|_{M,D} = \sup_{v \in \mathbb{R}^p \backslash \{0\}} \frac{\| T v \|}{\| v \|_M}\).

2.9 Pertinence de l’ACP - Choix de la dimension

2.9.1 Test de Bartlett

Est-il pertinent de réduire la dimension de représentation des données dont on dispose?

• L’hypothèse nulle est \[ (H_0):\ \lambda_k=1\ \forall k \]

• Statistique de test: \[ -\left(n-1-\dfrac{2p+5}{6}\right)\sum_{k=1}^p\ln\lambda_k\underset{(H_0)}{\sim}\mathcal{X}_{\left[\frac{p(p-1)}{2}\right]}^2 \]

2.9.2 Choix de la dimension de représentations graphiques

• Si le but de l’ACP est tout simplement représenter graphiquement les données, on choisira \(q\in\left\{2, 3\right\}\);

• Sinon il faut tenir compte de la part de variabilité expliquée par \(E_q\).

• De nombreux critères de sélection de \(q\) sont proposées dasn la littérature

2.9.3 Ébouli des valeurs propres

• Repose sur la recherche du 1er “coude” de décroissance des valeurs propres

• Ce coude peut être difficile à identifier, en particulier lorsque les variables sont faiblement correlées.

2.9.4 Seuillage de la qualité de représentation

• La part de l’inertie expliquée par \(E_q\) est \[r_q=\dfrac{\sum_{j=1}^q\lambda_j}{\sum_{j=1}^r\lambda_j}.\]

• On sélectionne la plus petite dimension \(q\) pour laquelle \(r_q\) est \(\geq\) à un seuil fixé a priori par l’utilisateur.

2.9.5 Règle de Kaiser (simple)

• Repose sur l’idée qu’un axe est intéressant lorsque sa variabilité (valeur propre associée) est supérieure à la moyenne.

• Pour une ACP normée, la moyenne des valeurs propres vaut \(1\).

Note: Ce critère ne tient pas compte des dimensions des données.

2.9.6 Règle de Kaiser (améliorée)

Pour une ACP normée, le seuil de la qualité de représentation est: \[1+2\sqrt{\dfrac{p-1}{n-1}}\]

2.9.7 Test bâtons brisés

Repose sur l’idée que si l’inertie totale était distribuée uniformément sur les axes, la distribution des valeurs propres suivrait la loi des “bâtons brisés”.

• Valeur seuille pour la \(k\)ième valeur propre: \(b_k=\sum_{h=k}^p\dfrac{1}{h}\)

• Dans la pratique, on compare \(k\mapsto\lambda_k\) et \(k\mapsto b_k\) dans le même graphique, et on considère les \(\lambda_k>b_k\).

2.10 Aide à l’interprétation de l’ACP

1. Les axes factoriels sont interprétés par rapport aux variables qui y sont bien représentées.

2. Les graphiques des individus sont interprétés en tenant compte des qualités de représentation, en termes de regroupement ou de dispersion par rapport aux axes principaux.

3. Les contributions des individus permettent d’identifier ceux qui ont une grande influence sur l’ACP. Ces individus sont à vérifier, et éventuellement à considérer comme supplémentaires dans une autre analyse.

4. Pour décrire une carte des variables ou des individus, on adoptera le plan suivant :

   1. Donner le pourcentage d’inertie expliqué par chaqye axes;

   2. Indiquer les variables (resp.les individus) mal représenté(e)s pour les exclure de la description ;

   3. Utiliser les contributions

   • des variables pour interpréter les axes en termes de variables de départ
   • des individus pour identifier ceux qui sont influents pour l’orientation d’un axe et ceux qui ont une contribution excessive. Ces individus sont source d’instabilité (le fait d’enlever de tels individus de l’analyse modifie de manière importante les résultats). Il est important de vérifier qu’il ne s’agit pas de données erronées et de faire une nouvelle analyse en les considérant en supplémentaires.

5. Pour une carte des variables : étudier les angles entre les projections des variables en termes de covariance ou de corrélation dans le cas d’une ACP normée pour dégager éventuellement des groupes de variables. Vérifier les tendances visualisées sur la carte par un examen de la matrice de corrélation.

6. Pour une carte d’individus : étudier les proximités ou les oppositions entre les points en termes de “comportement” et dégager éventuellement des groupes d’individus et des comportements singuliers de certains. Vérifier les caractéristiques dégagées par un examen des données de départ.

7. Faire une synthèse des informations et hypothèses principales dégagées de la carte décrite.

2.11 Exemples

2.11.1 Exemple sur les données iris

2.11.1.1 Sous R

Nous allons considéré les données iris. Elles sont constituées des dimensions des sépales et de celles des pétales de trois espèces de fleurs iris. Voici les \(5\) premières lignes du jeu de données.

iris |> 
  head(n=5)

iris[, 5] |>
  table() |>
  barplot()

Données des données pour l’ACP

X = as.matrix(iris[, 1:4])

Données centrées

Y = scale(X, center = TRUE, scale = FALSE)

Poids

n = nrow(iris)
D = diag(x = 1/n, nrow = n)

Métrique

# Matrice des variances
S2 = t(Y) %*% D %*% Y

# Métrique
M = diag(1/diag(S2))

Matrice \(S^2M\)

S2M = S2 %*% M

Décomposition spectrale

Voir la fonction eigen

decomp = eigen(S2M)

lambdas = decomp$values

V_tilde = decomp$vectors

normesV =  t(V_tilde) %*% M %*% V_tilde |> 
  diag() |>
  sqrt() |>
  as.matrix()

xx = matrix(1, ncol = 1, nrow = 4) %*% t(normesV)

V = V_tilde/xx

Composantes principales

CP = Y %*% M %*% V

Facteurs principaux

Lambda = diag(lambdas)
LambdaPuisMoins05 = diag(1/sqrt(lambdas))
FP = CP %*% LambdaPuisMoins05

Composantes principales des variables

CPV = V %*% sqrt(Lambda)

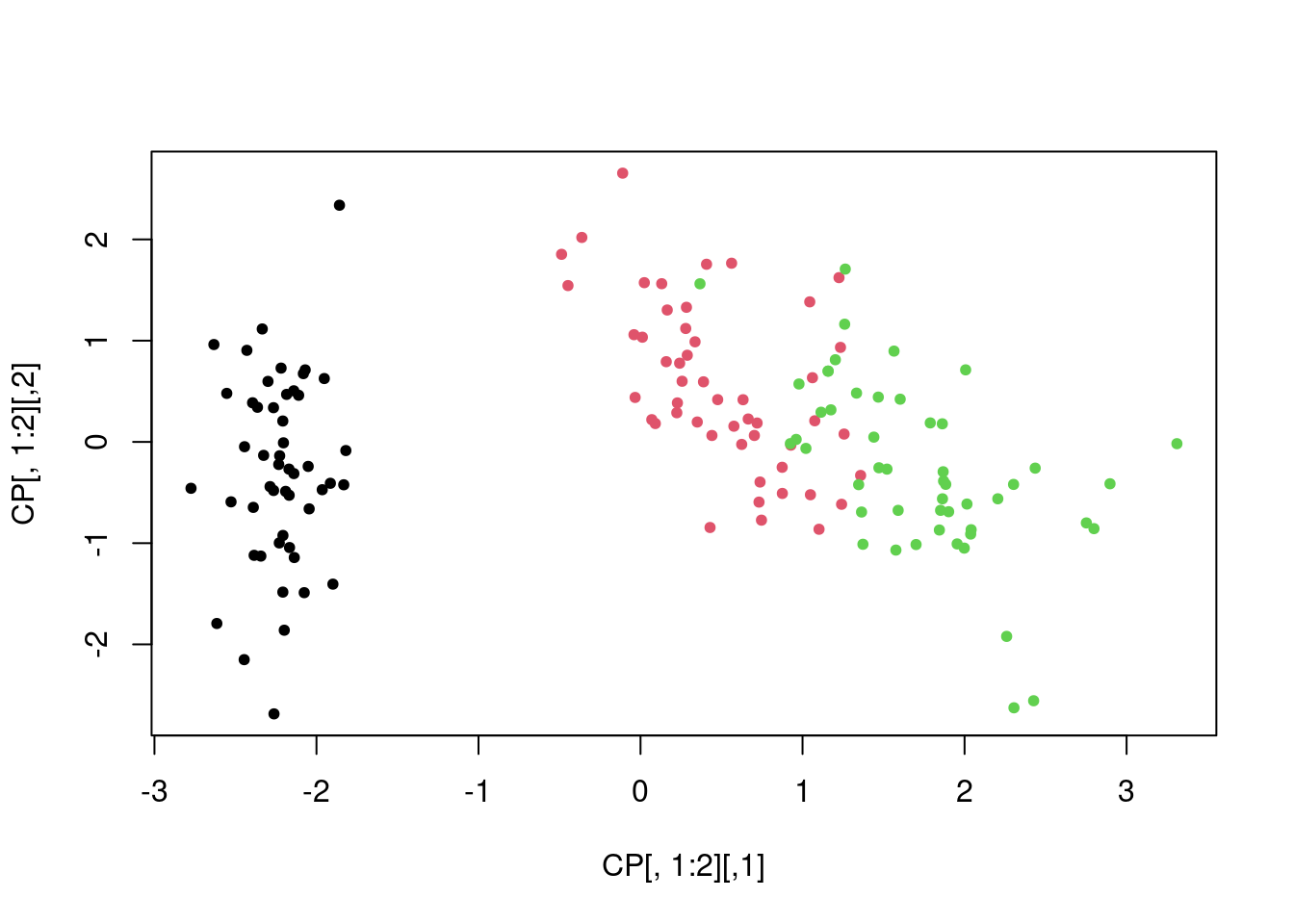
Nuage des individus dans le premier plan principal

plot(CP[, 1:2], pch = 20, col = iris$Species)

require(ggplot2)
ggplot(mapping = aes(x = CP[, 1], y = CP[, 2], color = iris$Species)) +
  geom_point()

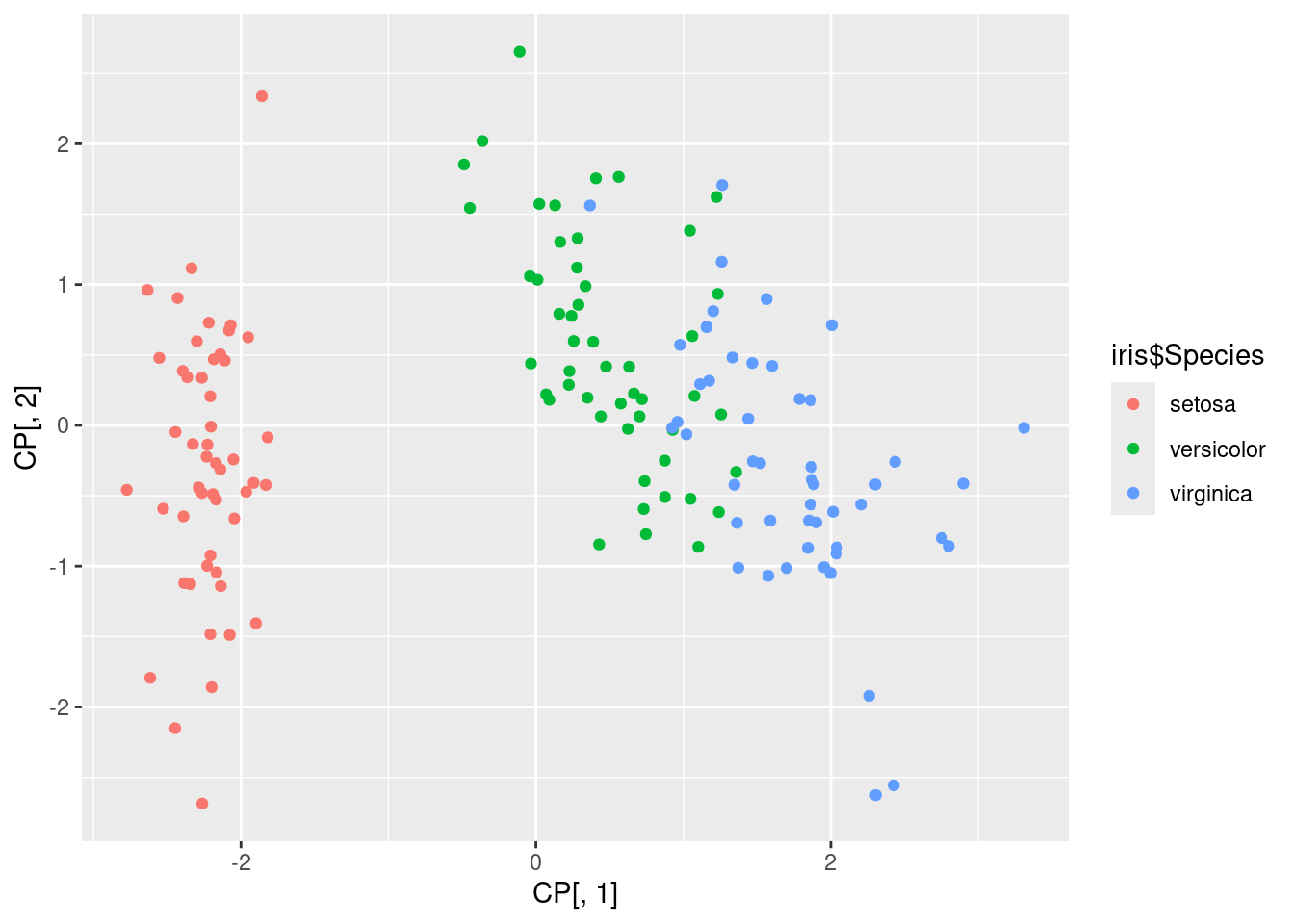
Les pourcentages des inerties expliquées

lambdas/sum(lambdas)*100

[1] 72.9624454 22.8507618  3.6689219  0.5178709

Qualité de représentation dans \(E_2\)

sum(lambdas[1:2])/sum(lambdas)

[1] 0.9581321

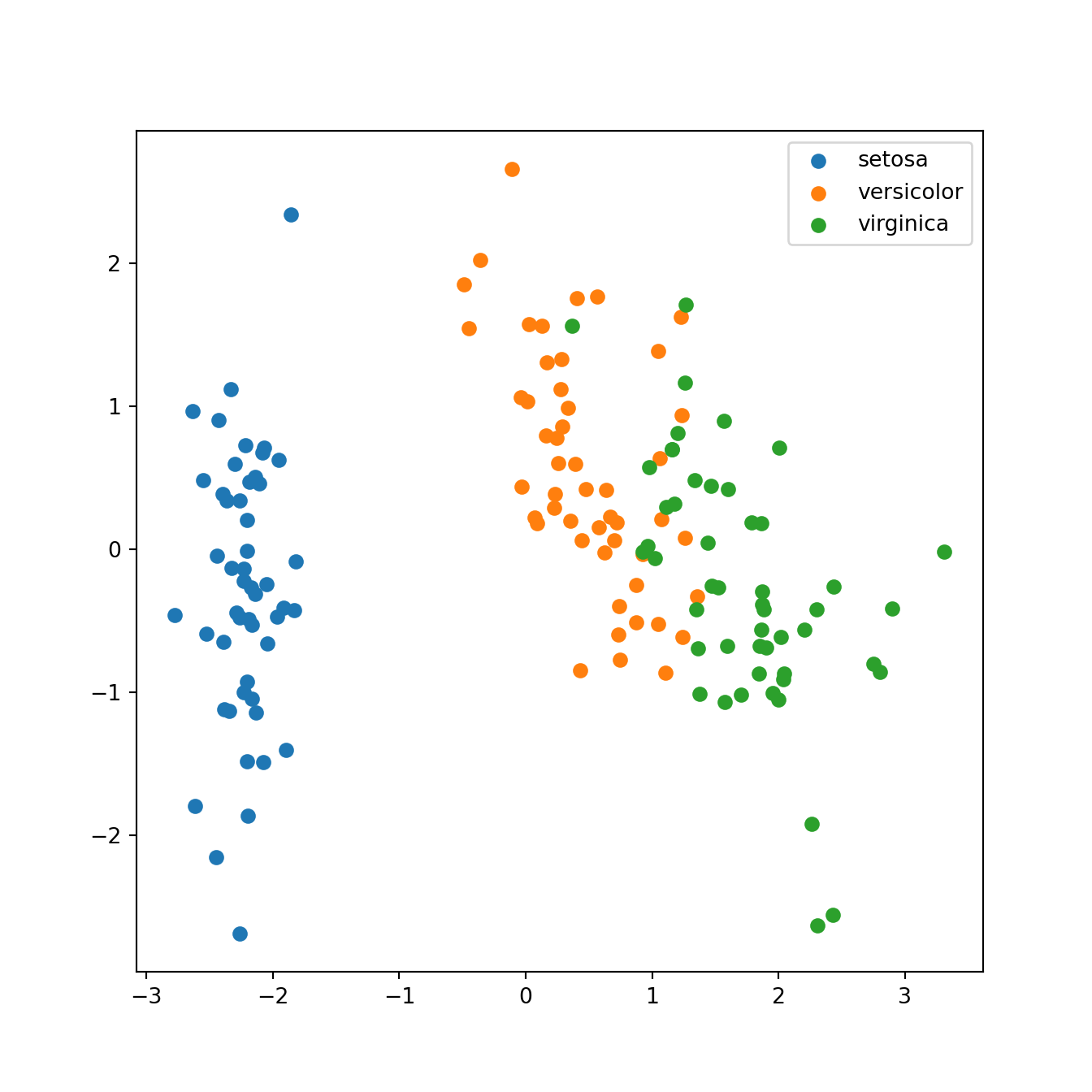
Commentaire: Le premier plan principal explique plus de \(95\%\) de la variabilité. Les conclusions qu’on peut en tirer sont donc très pertinentes.

Conclusions par rapprot au 1er plan principal

• Le 1er plan principal discrimine clairement l’espèce setosa par rapport aux deux autres;

• Les deux autres espèces sont assez bien discriminées dans ce plan là;

• On peut même noter que le premier axe principal discrimine clairement l’espèce setosa.

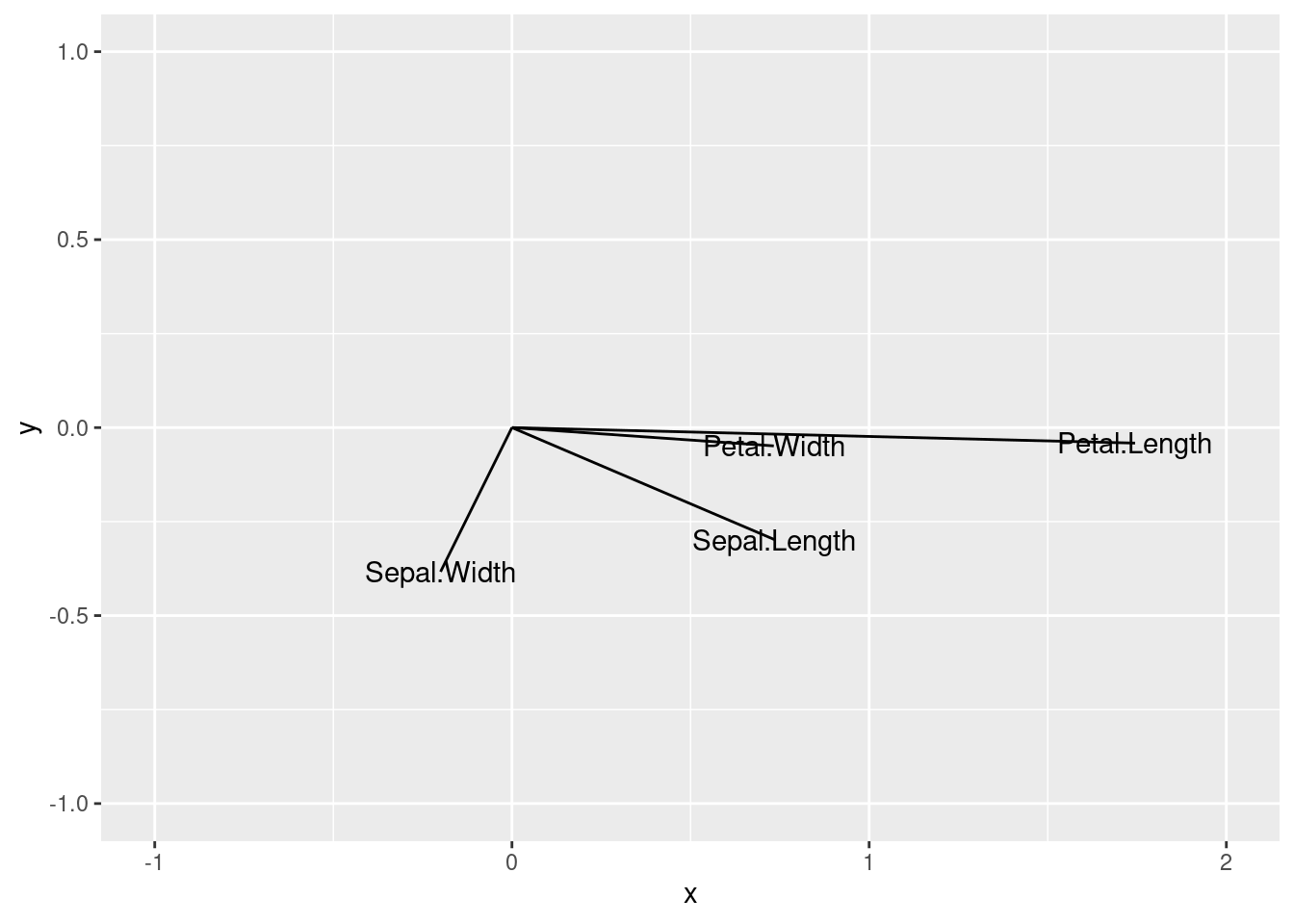
Représentation des variables dans le 1er plan principal

varNames = names(iris)[-5]

CPV = as.data.frame(CPV)
names(CPV) = paste("c", 1:4, sep="")
row.names(CPV) = varNames

ggplot(data = CPV) +
  xlim(-1, 2) +
  ylim(-1, 1) +
  geom_segment(mapping = aes(x = 0, y = 0, xend = c1, yend = c2)) +
  geom_text(mapping = aes(x = c1, y = c2, label = varNames))

2.11.1.2 Sous Python

import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from numpy import linalg

Ma classe ACP

Charger les données

iris0 = datasets.load_iris()
iris = pd.DataFrame(iris0.data, columns = iris0.feature_names)
iris['Species'] = iris0.target_names[iris0.target]
iris.head()

   sepal length (cm)  sepal width (cm)  ...  petal width (cm)  Species
0                5.1               3.5  ...               0.2   setosa
1                4.9               3.0  ...               0.2   setosa
2                4.7               3.2  ...               0.2   setosa
3                4.6               3.1  ...               0.2   setosa
4                5.0               3.6  ...               0.2   setosa

[5 rows x 5 columns]

# Les données
X = iris0.data

# Réduire les données
Y = StandardScaler(with_mean=True, with_std = False).fit_transform(X)

# Nombre d'indiviuds
n = X.shape[0]

# Matrice des poids
D = np.diag([1/n for i in range(n)])

# Matrice des variances
S2 = (Y.T).dot(D).dot(Y)

# Métrique usuelle
M = np.diag(1/np.diag(S2))

# Matrice à décomposer
S2M = S2.dot(M)

# Valeurs et vecteurs propres non M-normés
lambdas, U_tilde = linalg.eig(S2M)

# Normer les vecteurs propres
normesU = np.sqrt (np.diag(U_tilde.T.dot(M).dot(U_tilde))).reshape((4, 1))
xx = np.ones((4, 1)).dot(normesU.T)
U = U_tilde/xx

# Composantes principales
CP = Y.dot(M).dot(U)

# Matrice des valeurs propres
Lambda = np.diag(lambdas)

# LambdaInv05
LambdaInv05=np.diag(1/np.sqrt(lambdas))

# Lamnda05
Lambda05 = np.diag(np.sqrt(lambdas))

# Facteurs principaux
F = CP.dot(LambdaInv05)

# Composantes principales pour les variables
CPV = U.dot(Lambda05)

# Inertie expliquée
lambdas[0:2].sum()/lambdas.sum()

0.9581320720000165

Nuage des individus

plt.figure(figsize=(7, 7))
for species in iris0.target_names:
  indices = iris.Species == species
  plt.scatter(CP[indices, 0], CP[indices, 1], label = species)
  
plt.legend(loc = "best")
plt.show()

2.11.2 Données decathlon

Données

require(dplyr)

decathlon = read.csv(file = "../../data/decathlon.csv", sep = ";")

decathlon %>%
  select(-Classement, -Points, -X) -> df

row.names(df) = decathlon$X

df %>% head()

ACP

require(FactoMineR)
require(factoextra)

acp = PCA(df, scale.unit = TRUE, quali.sup = c(11), graph = FALSE)

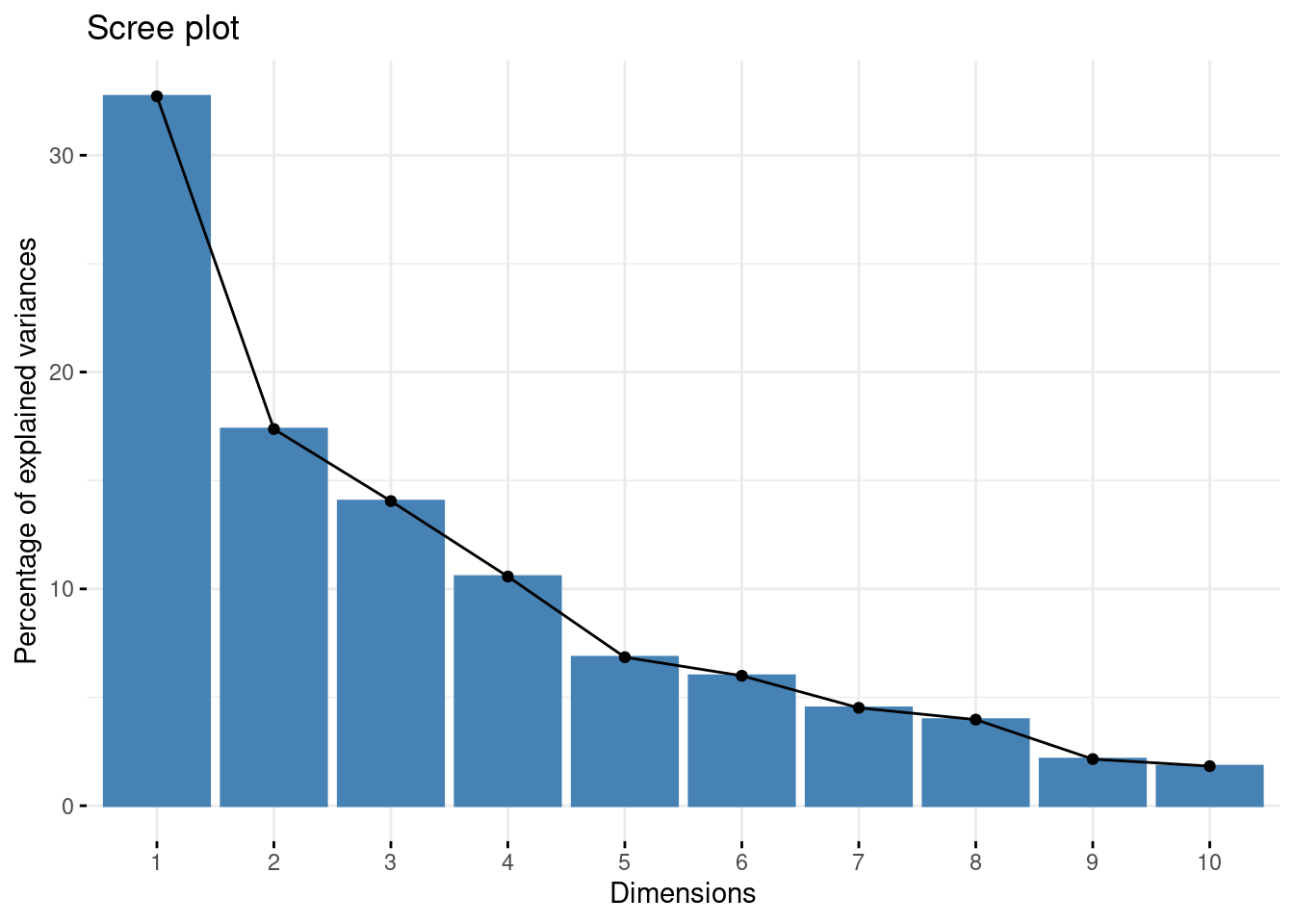
Ébouli des valeurs propres

fviz_screeplot(acp) 

Pourcentage de l’inertie expliquée par chaque composante

p = ncol(df) - 1
acp$eig[, 1]*10 

   comp 1    comp 2    comp 3    comp 4    comp 5    comp 6    comp 7    comp 8 
32.719055 17.371310 14.049167 10.568504  6.847735  5.992687  4.512353  3.968766 
   comp 9   comp 10 
 2.148149  1.822275 

Pourcentage de l’inertie expliquée par les espaces principaux

acp$eig[,1] |> 
  cumsum() * 100/p

   comp 1    comp 2    comp 3    comp 4    comp 5    comp 6    comp 7    comp 8 
 32.71906  50.09037  64.13953  74.70804  81.55577  87.54846  92.06081  96.02958 
   comp 9   comp 10 
 98.17773 100.00000 

Note

• Les 2 premiers axes principaux expliquant plue de \(50\%\) de l’inertie.

• D’après l’ébouli des valeurs propres, le choix de la dimension \(2\) est pertinent.

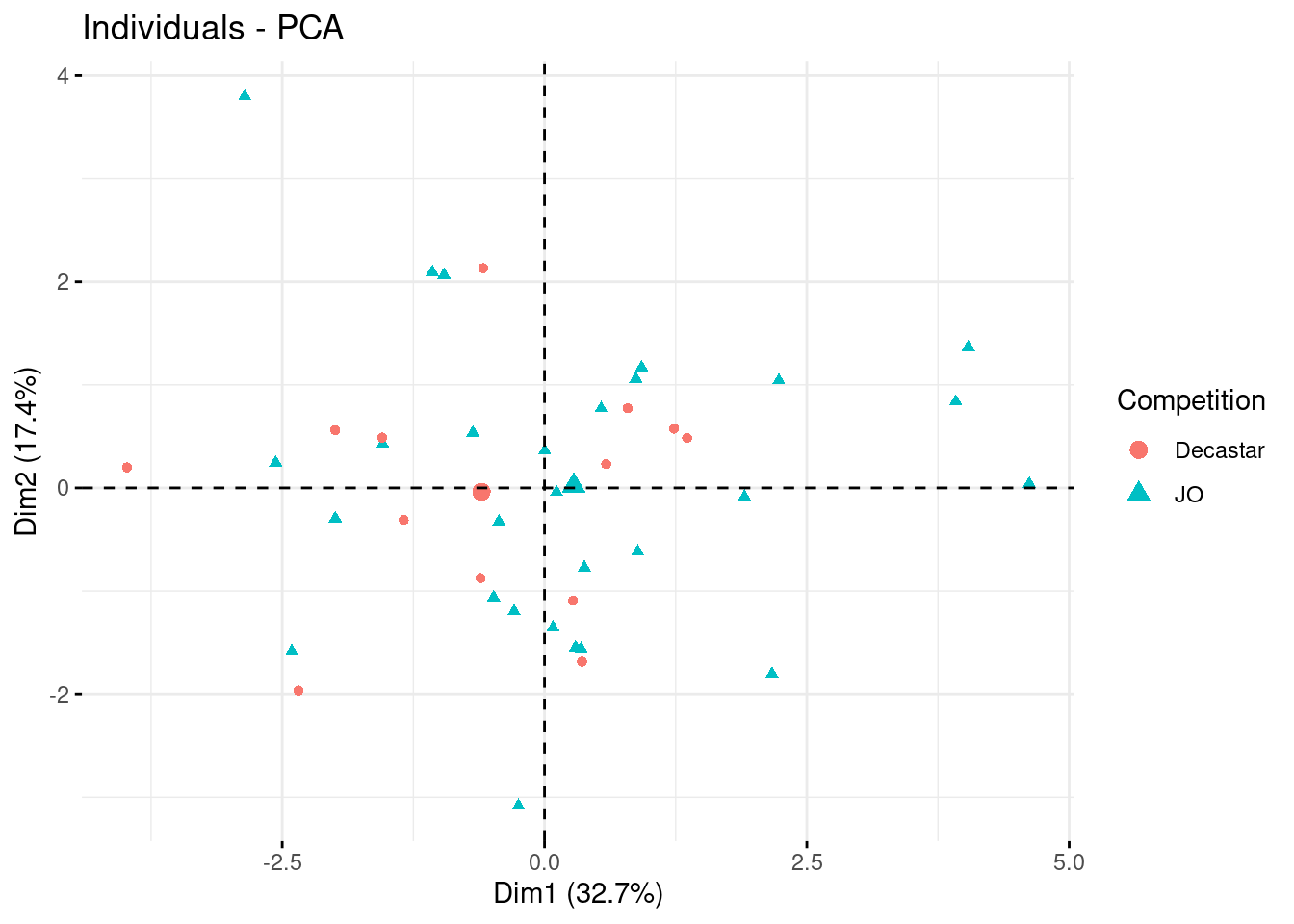
Représentation des individus

fviz_pca_ind(
  acp, 
  geom = "point", 
  axes = c(1, 2),
  habillage = "Competition"
)

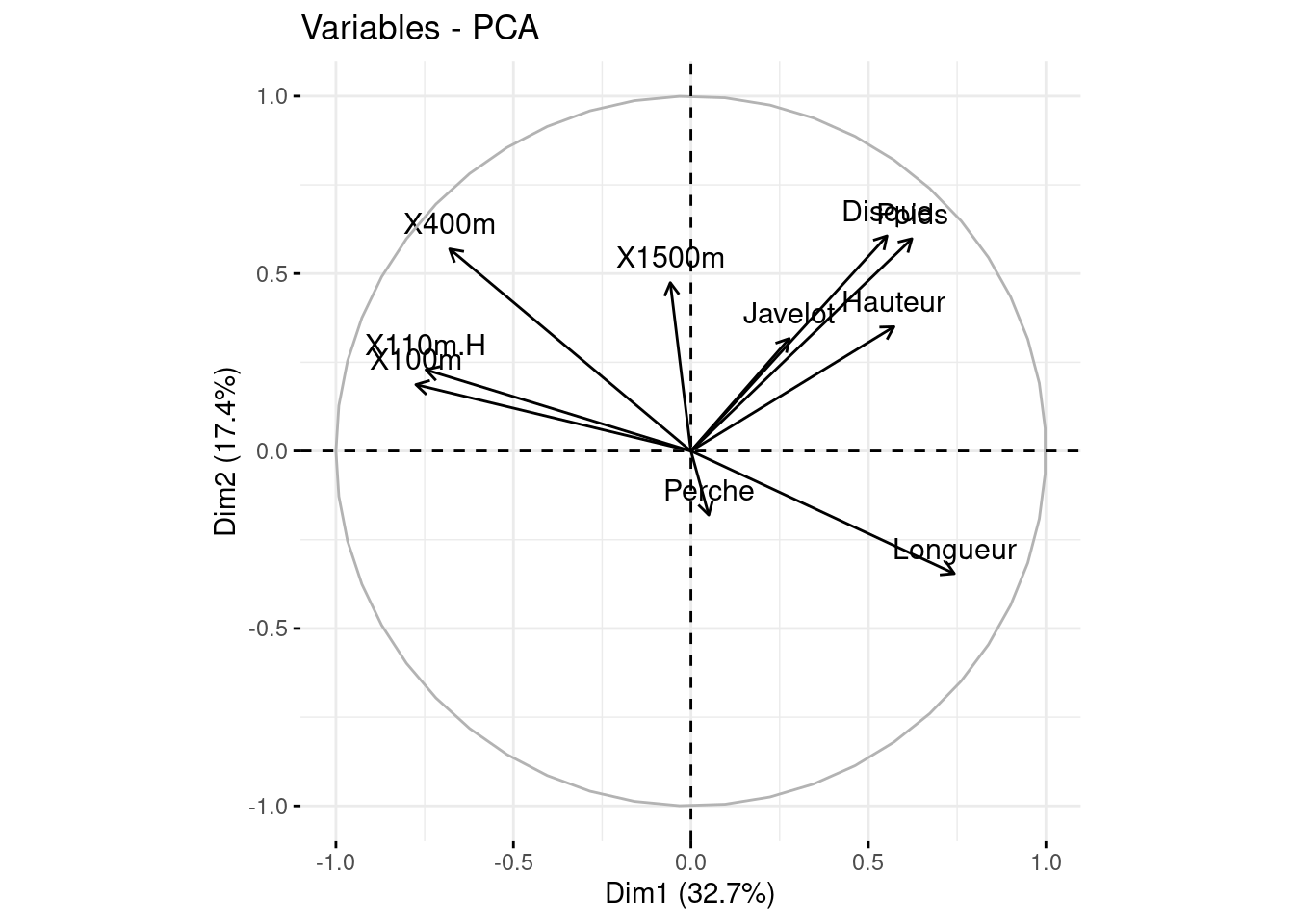
Représentation des variables dans le cercle des corrélations

fviz_pca_var(acp,  axes = c(1, 2))

Commentaires

• Les vaiables Perche et Javelot sont mal représentées dans ce plan, il faut alors se garder d’en tirer des conclusions;

• Les groupes de disciplines fortement positivement correlées:

  • X100m, X110.H

  • Disque, Poids, Hauteur

• X400m et Longueur sont très négativement correlées;

• Chacune des disciplines X100m et X110.H est décorrelée de Disque, Poids et Hauteur;

• Le premier axe oppose le groupe de disciplines Longueur, Poids, Hauteur et Disque au groupe X100m, X110m.H et X400m.

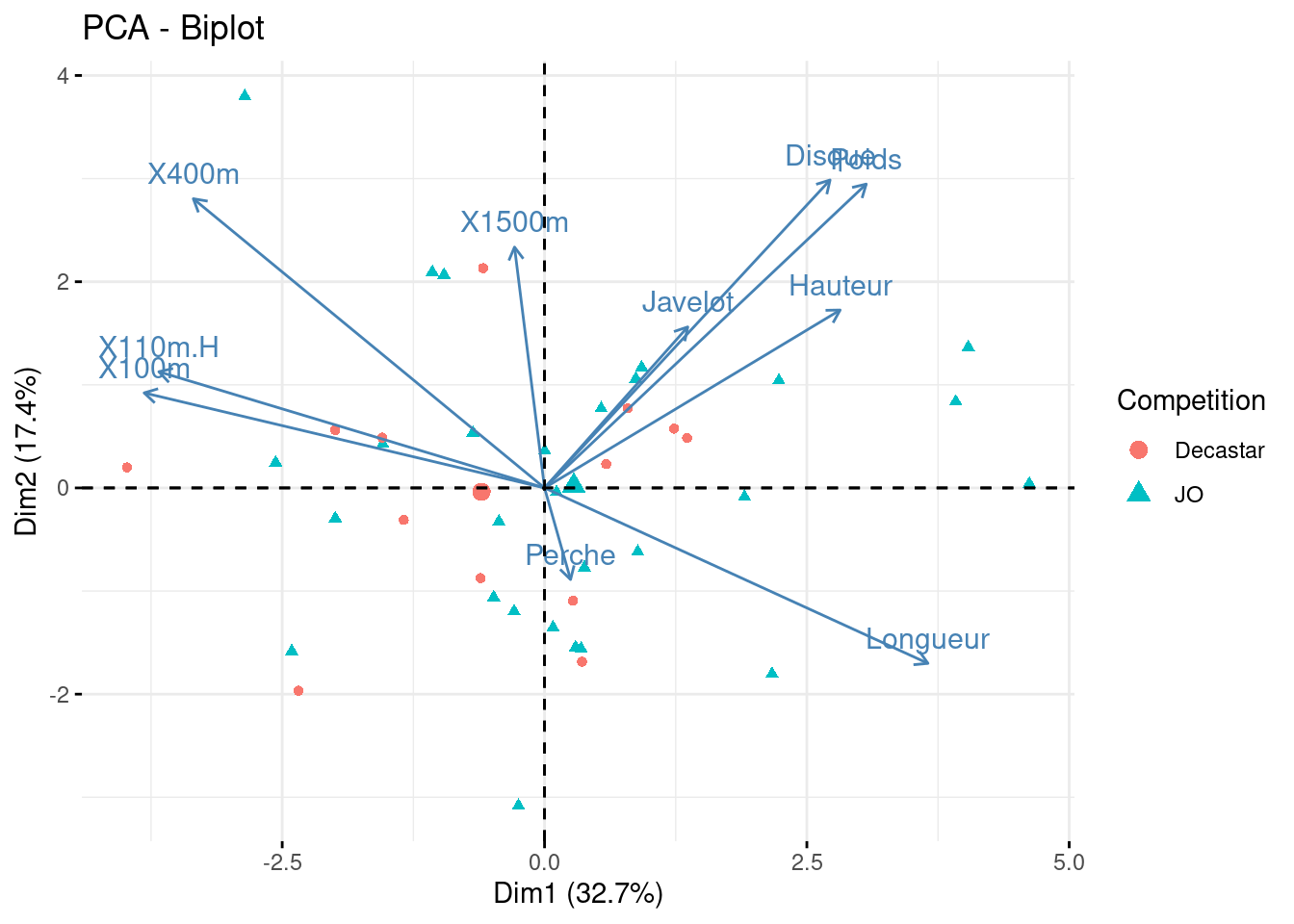
Bi-plot des individus et variables

fviz_pca_biplot(
  acp,
  label = "var",
  axes = c(1, 2),
  habillage = "Competition"
)

2.12 Exercices

Exercise 2.1 (ACP des individus) Rappelons que le jeu de données se présente sous la forme d’une matrice \(X = (x_{i,j})\), de dimensions \(n \times p\), à coefficients dans \(\mathbb{R}\), où \(n\) est le nombre d’individus et \(p\) celui des variables.

• L’espace \(\mathbb{R}^n\) des individus d’une métrique \(M\);
• L’espace \(\mathbb{R}^p\) des variables d’une métrique \(D = diag(w_1, \ldots, w_n)\) où \(w_i > 0\) et \(\sum_{i} w_i = 1\).

Nous notons \(Y = (y_{i,j})\) la matrice des données centrées, et \(Z = (z_{i,j})\) celle des données centrées réduites.

1. Rappeler les liens entre \(Y\), \(Z\) et \(X\).

2. Déterminer la matrice \(S^2\) des variances-covariances des observations.

3. Soit \(u^1\) un vecteur \(M\)-unitaire qui engendre le premier axe principal.

   1. Montrer que l’inertie du nuage centré par rapport à cette axes est \(I_{u^1} = {}^tu_1MS^2 Mu_1\).

   2. Rappelons que \(u^1 = \arg\max_{\|u\|_{M}^2 = 1}I_{u^1}\). Montrer que \(u^11\) est un vecteur propre associé à la plus grande valeur propre \(\lambda_1\) de \(S^2M\).

   3. La première composante principale \(c^1\in\mathbb{R}^n\) est le vecteur des coordonnées des projectés \(M\)-orthogonaux des lignes de \(Y\) sur \(\Delta_{u^1}\), coordonnées dans la base \((u^1)\). Montrer que \(c^1=YMu^1\in\mathbb{R}^n\).

4. Le 2e axe principal est engendré par un vecteur \(u^2\) tel que \(I_{u^2}\) est maximale parmi les inerties expliquées par les droites \(\Delta_{u}\) où \({}^tuMu = 1\) et \({}^tuMu^1 = 0\). Montrer que \(u^2\) est un vecteur propre de \(S^2M\) associé à la deuxième plus grande valeur propre \(\lambda_2\) de \(S^2M\).

5. En déduire une caractérisation générale des axes principaux.

6. Pour obtenir la réduction de la dimension de représentation des individus à \(q\), il suffit de projeter \(M\)-orthogonalement les individu centré \(y_i\) dans l’espace principal \(E_q=Vect\left\{u^1,\cdots,u^q\right\}\).

   1. Vérifier que les coordonnées de la projection des \(n\) individus centrés sont données dans les \(q\) premières colonnes de \(C=YMU\).

   2. Montrer que les colonnes de \(C\) sont centées, décorrelées et de variance la diagonale de la matrice \(\Lambda=diag(\lambda_1,\cdots,\lambda_r)\).

Exercise 2.2 (ACP des variables) L’ACP des individus est notée \(ACP\left(Y, D, M\right)\) où:

• \(Y\) est la matrice des données

• \(D\) la matrice des poids

• \(M\) la métrique.

L’ACP des variables est par \(ACP({}^tY, M, D)\). Ainsi, la matrice à décomposer pour cette ACP est \[ YM{}^tYD. \]

Supposons que \(rg(Y)=r\).

1. Montrer que \(YM{}^tYD\) et \(S^2M\) ont les mêmes valeurs propres non-nulles \(\lambda_1>\cdots>\lambda_r>0\) que \(S^2M\), de vecteurs propres associés donnés par les colonne de la matrice \(F=C\Lambda^{-\frac{1}{2}}\).

2. Montrer que les colonnes de \(F\) sont \(D\)-orthonormés.

3. Montrer que la matrice des composantes principales est \(C_{pv}=U\Lambda^{\frac{1}{2}}\).

4. Montrer que la matrice des facteurs principaux est \(F_{pv}=U\).

5. Montrer que la part de l’inertie expliquée par les espaces principaux des deux ACP sont égales.

6. Dresser un tableau comparatif de l’ACP des variables à celle des individus.

Exercise 2.3 On dispose du classement de \(n = 11\) individus sur \(p = 3\) matières : math, musique et français. Le classement en math revient à numéroter les individus. Le tableau des classements selon les trois matières est donné dans la Table 2.

Matière	1	2	3	4	5	6	7	8	9	10	11
Math	6	1	4	5	3	2	9	7	8	10	11
Musique	6	1	4	5	3	2	9	7	8	10	11
Français	2	6	5	3	4	1	8	9	7	10	11

Les individus sont affectés du même poids.

1. Calculer le centre de gravité \(\bar{x}\).
2. Calculer le tableau des données centrées \(Y\).
3. 1. Réaliser l’ACP des individus.
   2. Réaliser l’ACP des variables.
   3. Commenter les résultats.
4. Vérifier les calculs à l’aide du logiciel R ou Python.

Exercise 2.4 On considère un jeu de données \(X = (x_{ij})\) constitué de deux séries statistiques quantitatives \(x^1\) et \(x^2\). La matrice de variances-covariances empirique est

\[ S^2 = \begin{pmatrix} 1 & \alpha \\ \alpha & 1 \end{pmatrix} \]

où \(\alpha > 0\). On note \(\lambda_1 \ge \lambda_2\) les deux valeurs propres de \(V\). On munit l’espace \(\mathbb{R}^2\) des individus du produit scalaire usuel.

1. Calculer \(\lambda_1\) et \(\lambda_2\).
2. Calculer les deux vecteurs propres orthogonaux et unitaires \(u^1\) et \(u^2\) de \(S^2\).
3. Calculer les composantes principales \(c^1\) et \(c^2\) en fonction de \(x^1\), \(x^2\) et éventuellement de \(\alpha\).
4. En déduire la moyenne et la variance de \(c^1\) et \(c^2\).
5. On note \(C\) la matrice de colonnes \(c^1\) et \(c^2\) et \(V\) celle de colonnes \(u^1\) et \(u^2\). Montrer que \(c^1\) et \(c^2\) sont non-corrélées.

Exercise 2.5 (Travaux pratiques) Ce TP vise à appliquer l’ACP sur le jeu de données iris, qui est un ensemble de données classique en statistiques et contient les mesures en centimètres de la longueur et de la largeur des sépales et des pétales pour 50 fleurs de chacune des \(3\) espèces d’iris.

Objectifs

• Comprendre et appliquer l’ACP pour réduire la dimensionnalité des données.
• Visualiser les données dans le nouvel espace des composantes principales.
• Interpréter les axes principaux et les scores des composantes.

Matériel Nécessaire

• Langages R ou Python;
• IDE: RStudio ou jupyter;
• Les packages FactoMineR et ggplot2 sous R;
• Les librairies scikit-learn, pandas, numpy, matplotlib sous Python.

Exploration des données

1. Chargez le jeu de données iris disponible dans R.
2. Réalisez une analyse exploratoire des données :
   • Calculez les statistiques descriptives de base.
   • Créez des graphiques de dispersion pour chaque paire de variables.

Prétraitement des Données

1. Standardisez les données en centrant et réduisant les variables pour que chacune ait une moyenne de zéro et un écart type de un.
2. Vérifiez que la standardisation est correcte en vérifiant les moyennes et les écarts types post-standardisation.

ACP sur les Données Iris

1. Utilisez le package FactoMineR pour effectuer une ACP normée sur le jeu de données iris.
2. Extrayez et interprétez les valeurs propres : combien de composantes principales retiendriez-vous et pourquoi ?

Visualisation des Composantes Principales

1. Visualisez les deux premières composantes principales avec ggplot2. Utilisez les couleurs pour distinguer les espèces d’iris.
2. Que pouvez-vous déduire de cette visualisation en termes de séparation des espèces ?

Interprétation des Résultats

1. Interprétez les vecteurs propres des deux premières composantes principales : quelles variables contribuent le plus à ces composantes ?
2. Comment les résultats de l’ACP peuvent-ils être utilisés pour une analyse plus poussée, comme la classification ?

Conclusion

Rédigez un bref rapport résumant les étapes effectuées, vos observations et conclusions sur la séparabilité des espèces dans le jeu de données iris à l’aide de l’ACP.

Exercise 2.6 (Implémentation sous R ou Python) Sous R

1. Implémentez une fonction myACP qui réalise l’ACP sur un jeu de données.

2. Comparez vos resultats à ceux que propose le package FactoMiner.

Sous Python

Le module preprocessing de la librairie scikit-learn contient une classe nommée PCA pour réaliser les calculs essentiels de l’ACP.

1. Explorer la classe PCA en notant les calculs effectués.

2. Créer une classe MyPCA qui hérite de PCA pour bénéficier des caluls de cette dernière, puis étendez les fonctionnalités en implémentant les méthodes complémentaires.

3. Tester votre classe sur les données iris qui se trouve dans le module datasets de scikit-learn.

Analyser les données suivantes sous R ou Python.

Modèle	CYL	PUISS	LONG	LARG	POIDS	V_MAX
Alfasud TI	1350	79	393	161	870	165
Audi 100	1588	85	468	177	1110	160
Simca 1300	1294	68	424	168	1050	152
Citroen GS Club	1222	59	412	161	930	151
Fiat 132	1585	98	439	164	1105	165
Lancia Beta	1297	82	429	169	1080	160
Peugeot 504	1796	79	449	169	1160	154
Renault 16 TL	1565	55	424	163	1010	140
Renault 30	2664	128	452	173	1320	180
Toyota Corolla	1166	55	399	157	815	140
Alfetta-1.66	1570	109	428	162	1060	175
Princess-1800	1798	82	445	172	1160	158
Datsun-200L	1998	115	469	169	1370	160
Taunus-2000	1993	98	438	170	1080	167
Rancho	1442	80	431	166	1129	144
Mazda-9295	1769	83	440	165	1095	165
Opel-Rekord	1979	100	459	173	1120	173
Lada-1300	1294	68	404	161	955	140

Exercise 2.7 Dans cet exercice, nous allons appliquer l’ACP à un jeu de données contenant les notes de \(n=15\) élèves dans quatre matières différentes : maths, physiques, français et latin, où chaque note est sur \(20\).

Élève	Maths	Physiques	Français	Latin
1	18	17	9	8
2	16	15	10	9
3	17	16	12	11
4	9	8	16	17
5	10	9	17	18
6	11	10	15	16
7	14	14	14	14
8	13	13	13	13
9	15	15	12	12
10	7	7	18	19
11	8	9	17	18
12	12	11	16	15
13	16	17	13	12
14	17	18	10	11
15	15	16	17	16

Les objectifs de cet exercice sont les suivants :

1. Standardisez les données et effectuez une ACP normée.
2. Combien de composantes principales faut-il retenir selon le critère de Kaiser ?
3. Interprétez les deux premières composantes principales : quels sont les contributions des variables originales dans ces composantes ?
4. Visualisez les élèves et les matières dans le permier plan principal.
5. Interprétez la position des élèves dans ce plan : y a-t-il des groupes d’élèves similaires ?