4  Latent Semantic Analysis: A SVD-based Approach

Code 
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.preprocessing import normalize
import matplotlib.pyplot as plt
import seaborn as sns

4.1 Document-Term Matrix Construction

4.1.1 Basic Principles

LSA starts with representing documents as vectors in a term space. Given a corpus of \(n\) documents and a vocabulary of \(p\) terms, we construct a document-term matrix \(X \in \mathbb{R}^{n\times p}\):

\[X = [x_{i,j}]\]

where \(x_{i,j}\) represents the importance of term \(j\) in document \(i\).

Code 
# Example corpus
corpus = [
    "machine learning algorithms",
    "deep learning neural networks",
    "statistical learning theory",
    "neural networks architecture",
    "statistical inference methods",
    "statistical descriptive methods",
]

# Create document-term matrix
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(corpus)
terms = vectorizer.get_feature_names_out()

# Display as dataframe
df = pd.DataFrame(X.toarray(), columns=terms)
print("Document-Term Matrix:")
df
Document-Term Matrix:
algorithms architecture deep descriptive inference learning machine methods networks neural statistical theory
0 0.635091 0.000000 0.000000 0.000000 0.000000 0.439681 0.635091 0.000000 0.000000 0.000000 0.000000 0.000000
1 0.000000 0.000000 0.595054 0.000000 0.000000 0.411964 0.000000 0.000000 0.487953 0.487953 0.000000 0.000000
2 0.000000 0.000000 0.000000 0.000000 0.000000 0.494686 0.000000 0.000000 0.000000 0.000000 0.494686 0.714542
3 0.000000 0.653044 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.535506 0.535506 0.000000 0.000000
4 0.000000 0.000000 0.000000 0.000000 0.681722 0.000000 0.000000 0.559022 0.000000 0.000000 0.471964 0.000000
5 0.000000 0.000000 0.000000 0.681722 0.000000 0.000000 0.000000 0.559022 0.000000 0.000000 0.471964 0.000000

4.1.2 TF-IDF Weighting

The term frequency-inverse document frequency (TF-IDF) weighting scheme is commonly used:

\[\text{tfidf}_{ij} = \text{tf}_{ij} \times \log(\frac{n}{df_j})\]

where:

  • \(\text{tf}_{ij}\) is the frequency of term \(j\) in document \(i\)
  • \(df_j\) is the number of documents containing term \(j\)
  • \(n\) is the total number of documents

4.2 SVD Decomposition in LSA

4.2.1 Mathematical Framework

LSA applies SVD to the document-term matrix:

\[X = U\Sigma V^T\]

where:

  • \(U \in \mathbb{R}^{n\times n}\) represents documents in the latent space
  • \(\Sigma \in \mathbb{R}^{n\times p}\) contains singular values
  • \(V \in \mathbb{R}^{p\times p}\) represents terms in the latent space
Code 
# Compute SVD
U, s, Vt = np.linalg.svd(X.toarray(), full_matrices=False)

# Plot singular values
plt.figure(figsize=(10, 4))
plt.plot(s, 'bo-')
plt.title('Singular Values in LSA')
plt.xlabel('Index')
plt.ylabel('Singular Value')
plt.grid(True)
plt.show()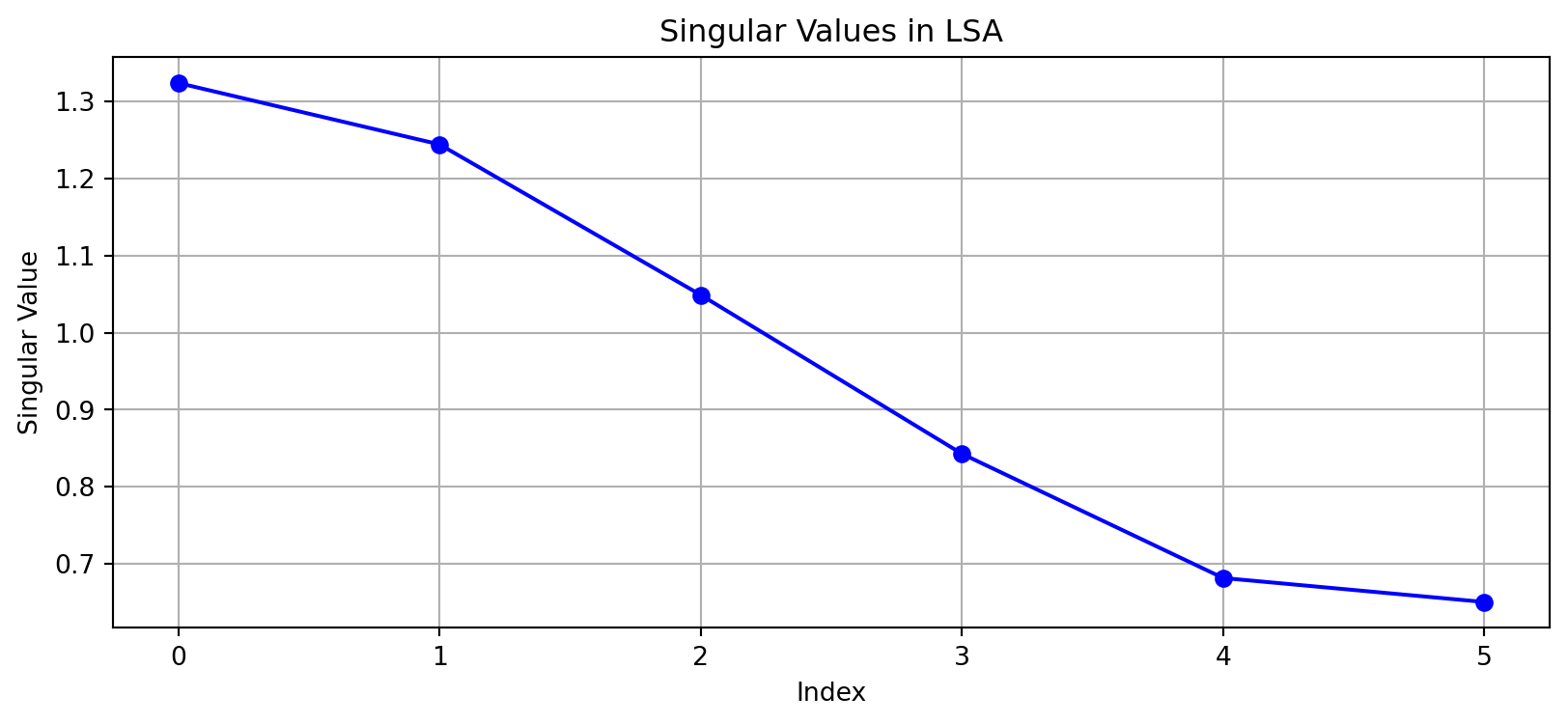

4.2.2 Dimensionality Reduction

LSA typically uses a truncated SVD to reduce to \(k\) dimensions:

\[X_k = U_k\Sigma_k V_k^T\]

This reduction:

  1. Captures main semantic relationships
  2. Reduces noise
  3. Reveals latent structure
Code 
def plot_semantic_space(U, terms, k=2):
    # Project terms into semantic space
    term_coords = Vt[:k, :].T
    
    plt.figure(figsize=(12, 6))
    
    # Plot terms
    plt.scatter(term_coords[:, 0], term_coords[:, 1], c='blue', alpha=0.5)
    for i, term in enumerate(terms):
        plt.annotate(term, (term_coords[i, 0], term_coords[i, 1]))
        
    plt.title(f'{k}D Semantic Space')
    plt.xlabel('First Dimension')
    plt.ylabel('Second Dimension')
    plt.grid(True)
    plt.show()
    return

# Plot 2D semantic space
plot_semantic_space(U, terms)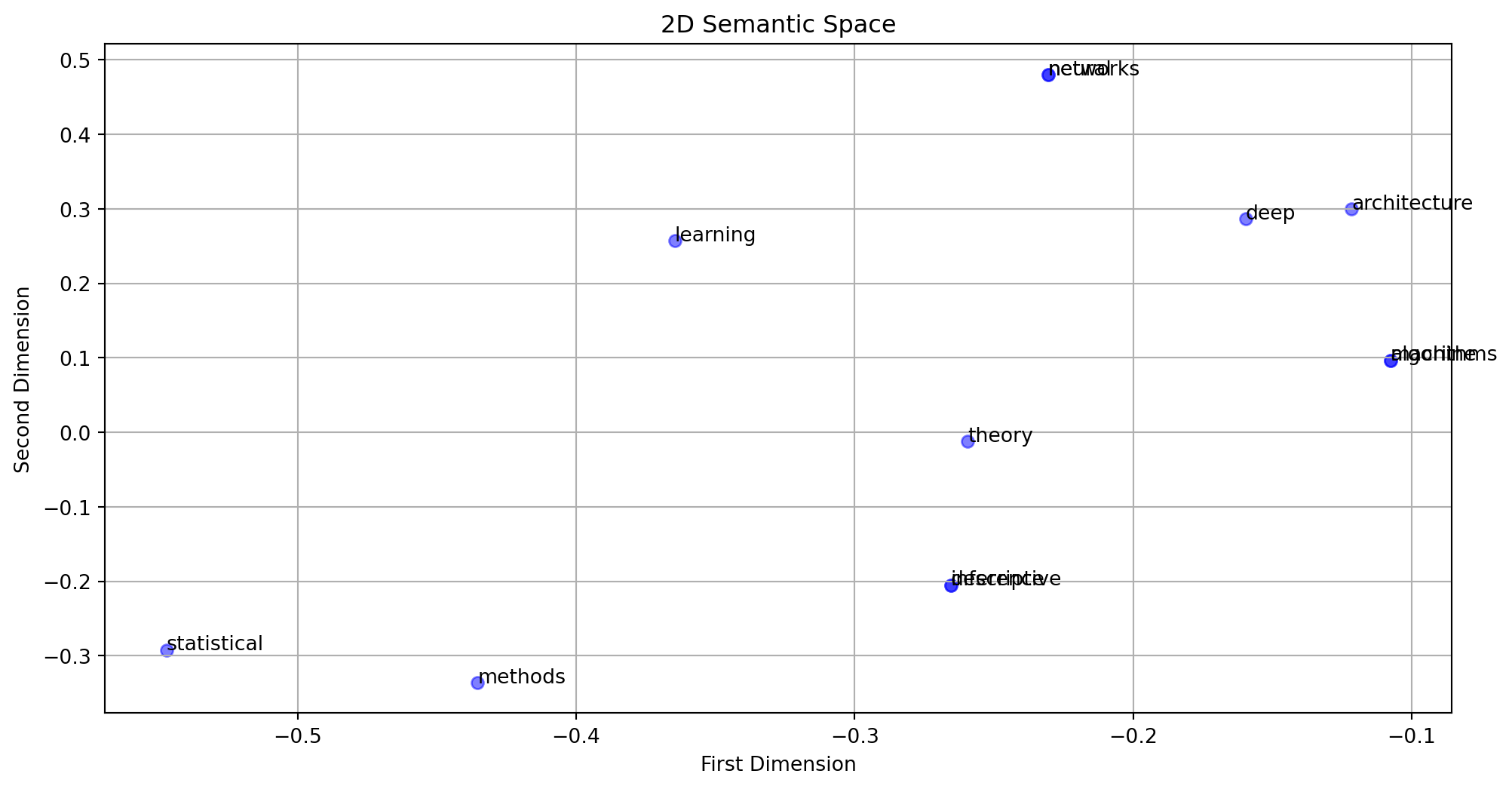

4.3 Applications

4.3.1 Document Similarity

We can compute document similarity in the reduced space:

Code 
def compute_doc_similarity(X_reduced):
    # Normalize documents
    X_norm = normalize(X_reduced)
    # Compute cosine similarity
    similarity = X_norm @ X_norm.T
    return similarity

# Reduce to k dimensions
k = 2
X_k = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]

# Compute and visualize similarities
sim_matrix = compute_doc_similarity(X_k)

plt.figure(figsize=(8, 6))
sns.heatmap(sim_matrix, annot=True, cmap='RdBu', center=0)
plt.title('Document Similarity Matrix')
plt.show()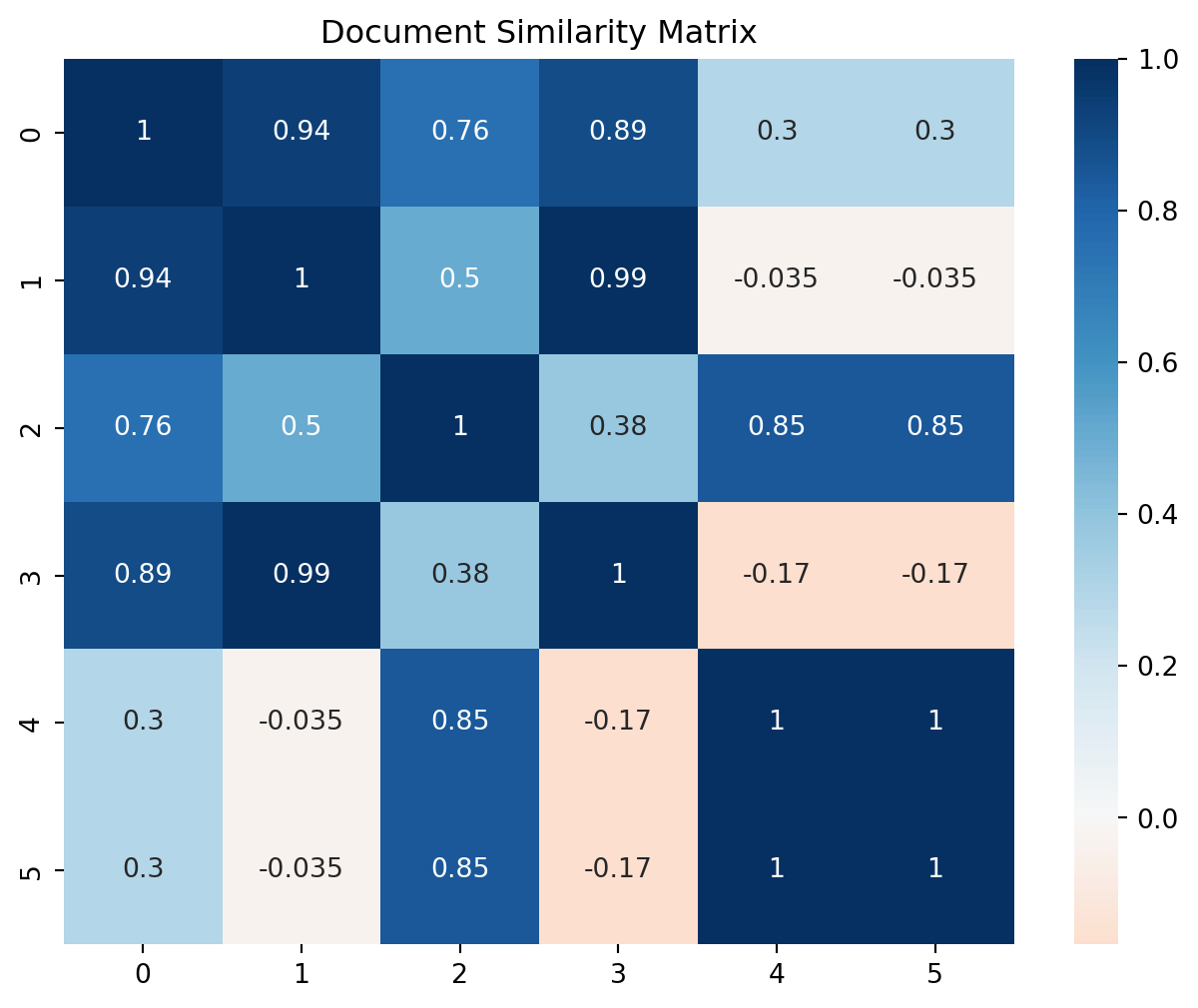

4.3.2 Query Processing

4.3.2.1 Query Projection

For a query vector \(q \in \mathbb{R}^p\), we project it into the LSA space:

\[q_k = q^T V_k \Sigma_k^{-1}\]

This gives us the query coordinates in the reduced concept space.

4.3.2.2 Document Similarity

The similarity between query and documents is computed as:

\[\text{sim}(q, d_i) = \frac{q_k \cdot d_{ik}}{||q_k|| \cdot ||d_{ik}||}\]

where \(d_{ik}\) is the \(i\)-th row of \(D_k\).

Code 
def process_query(query, vectorizer, Vk, Sk, Dk, k):
    # Convert query to TF-IDF vector
    q = vectorizer.transform([query]).toarray()
    
    # Project query to LSA space
    qk = q @ Vk[:, :k] @ np.diag(1/Sk[:k])
    
    # Compute similarities
    similarities = np.dot(qk, Dk[:, :k].T)
    similarities = similarities / (np.linalg.norm(qk) * 
                                np.linalg.norm(Dk[:, :k], axis=1))
    
    return similarities.flatten()

# Example query processing
k = 2  # number of dimensions to keep
Uk = U[:, :k]
Sk = s[:k]
Vk = Vt.T[:, :k]
Dk = Uk * Sk  # Document-concept matrix

query = "statistical"
similarities = process_query(query, vectorizer, Vt.T, s, Uk, k)

# Print results
for doc, sim in zip(corpus, similarities):
    print(f"Similarity: {sim:.3f} - {doc}")
Similarity: 0.346 - machine learning algorithms
Similarity: 0.019 - deep learning neural networks
Similarity: 0.890 - statistical learning theory
Similarity: -0.108 - neural networks architecture
Similarity: 0.994 - statistical inference methods
Similarity: 0.994 - statistical descriptive methods

4.3.2.3 Theoretical Properties

The LSA similarity measure has several important properties:

  1. Synonymy: Terms with similar meanings will have similar representations in the concept space:

\[\text{sim}(t_i, t_j) = \frac{(V_k\Sigma_k)_i \cdot (V_k\Sigma_k)_j}{||(V_k\Sigma_k)_i|| \cdot ||(V_k\Sigma_k)_j||}\]

  1. Polysemy: The reduced space can help disambiguate terms based on context:

\[\text{context}(t_i) = \sum_{j \in \text{docs}} u_{jk}\sigma_k v_{ik}\]

4.3.3 Choosing k

The optimal number of dimensions \(k\) can be chosen based on:

  1. Fraction of total variance explained:

\[\frac{\sum_{i=1}^k \sigma_i^2}{\sum_{i=1}^r \sigma_i^2} \geq \theta\]

  1. Rate of change in singular values:

\[\frac{\sigma_k - \sigma_{k+1}}{\sigma_k} \leq \epsilon\]

Code 
def plot_explained_variance(s):
    total_var = (s**2).sum()
    cum_var = np.cumsum(s**2) / total_var
    
    plt.figure(figsize=(8, 4))
    plt.plot(range(1, len(s) + 1), cum_var, 'b-o')
    plt.axhline(y=0.9, color='r', linestyle='--', label='90% threshold')
    plt.title("Cumulative Explained Variance")
    plt.xlabel("Number of components")
    plt.ylabel("Fraction of variance explained")
    plt.grid(True)
    plt.legend()
    plt.show()

plot_explained_variance(s)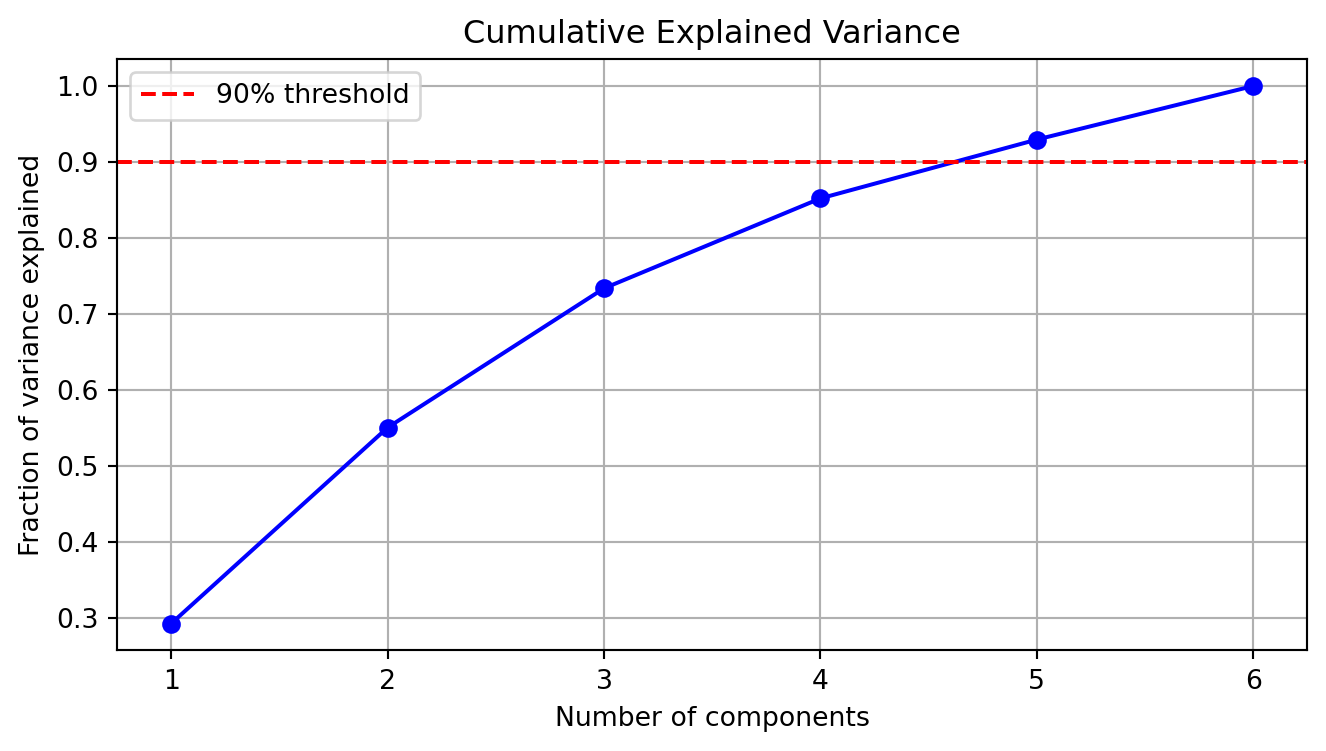

Key Points
  • LSA uses SVD to uncover latent semantic structure
  • Query processing involves projection into reduced space
  • Choice of k affects performance and computational cost
  • Similarity measures capture semantic relationships

4.4 References

4.5 Advanced Topics

4.5.1 Term Clustering

LSA can reveal term relationships through their positions in the semantic space:

Code 
from sklearn.cluster import KMeans

def plot_term_clusters(V, terms, k=2):
    
    # Use first k components
    term_coords = Vt[:k, :].T
    
    # Cluster terms
    kmeans = KMeans(n_clusters=3)
    kmeans.fit(term_coords)
    clusters = kmeans.predict(term_coords)
    
    plt.figure(figsize=(12, 6))
    scatter = plt.scatter(term_coords[:, 0], term_coords[:, 1], 
                         c=clusters, cmap='viridis')
    
    for i, term in enumerate(terms):
        plt.annotate(term, (term_coords[i, 0], term_coords[i, 1]))
        
    plt.title('Term Clusters in Semantic Space')
    plt.colorbar(scatter)
    plt.show()

#plot_term_clusters(Vt, terms)

4.5.2 Cross-Language LSA

LSA can be extended to multiple languages through parallel corpora:

Cross-Language LSA Steps
  1. Create parallel document-term matrices
  2. Perform SVD on concatenated matrices
  3. Project queries from one language to another

4.6 Practical Considerations

4.6.1 Choosing k

The choice of dimensionality \(k\) depends on: 1. Corpus size and sparsity 2. Computational resources 3. Application requirements

Code 
def plot_explained_variance(s):
    var_explained = np.cumsum(s**2) / np.sum(s**2)
    
    plt.figure(figsize=(10, 4))
    plt.plot(var_explained, 'bo-')
    plt.axhline(y=0.9, color='r', linestyle='--')
    plt.title('Cumulative Explained Variance Ratio')
    plt.xlabel('Number of Components')
    plt.ylabel('Cumulative Explained Variance')
    plt.grid(True)
    plt.show()

plot_explained_variance(s)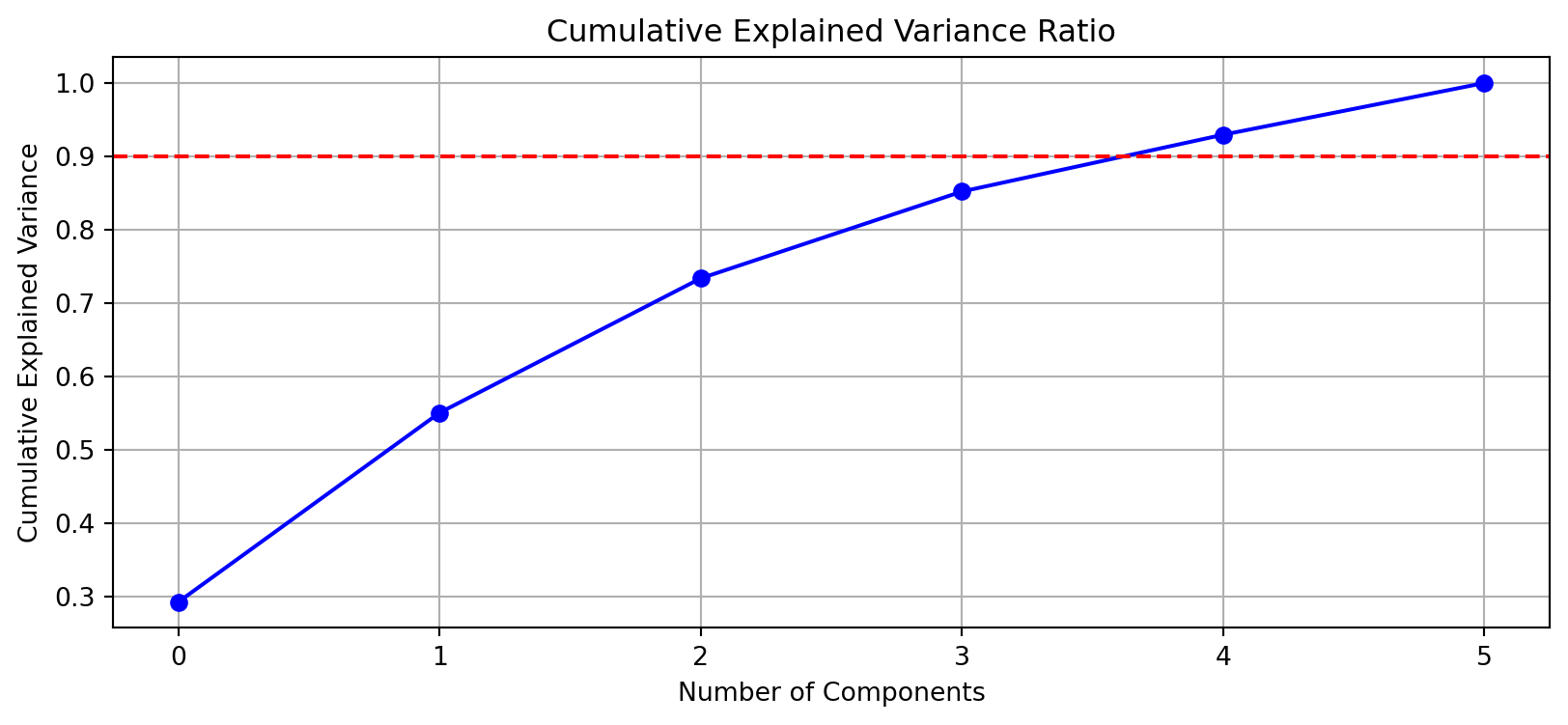

4.6.2 Preprocessing Impact

Text preprocessing significantly affects LSA results: - Stopword removal - Stemming/lemmatization - Case normalization - N-gram inclusion

4.7 Limitations and Extensions

LSA Limitations
  1. Assumes bag-of-words model
  2. Cannot handle polysemy well
  3. Topic interpretability
  4. Scale to very large corpora

Modern extensions include: - Probabilistic LSA (pLSA) - Latent Dirichlet Allocation (LDA) - Neural embeddings

4.8 References

  • Deerwester, S., et al. (1990). Indexing by latent semantic analysis
  • Manning, C. D., et al. (2008). Introduction to Information Retrieval
  • Berry, M. W., et al. (1995). Using Linear Algebra for Intelligent Information Retrieval