Le Clustering Hiérarchique : Construire l’Arbre Généalogique de vos Données

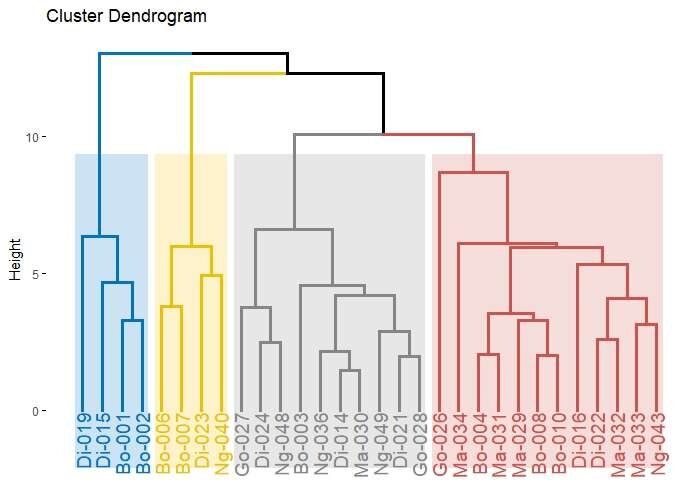
1 Introduction : Au-delà d’un Nombre Fixe de Clusters

Dans notre dernier article sur K-Means, nous avons vu un algorithme puissant mais qui nous obligeait à prendre une décision cruciale à l’avance : le nombre de clusters \(K\). De plus, K-Means peine à trouver des clusters qui ne sont pas de forme sphérique.

Et si nous pouvions explorer toutes les possibilités de regroupement, d’un seul grand groupe à autant de groupes qu’il y a d’observations ? Et si nous pouvions visualiser la “parenté” entre nos données ?

C’est exactement ce que propose le clustering hiérarchique. C’est une approche qui ne nécessite pas de choisir \(K\) au préalable et qui produit une visualisation incroyablement riche de la structure de nos données : le dendrogramme.

2 La Logique : Le Clustering Agglomératif (Bottom-Up)

Il existe deux types de clustering hiérarchique, mais le plus courant est de loin l’approche agglomérative (ou ascendante). L’intuition est très simple :

Départ : Au début, chaque point de données est considéré comme son propre cluster. Si nous avons \(n\) points, nous avons \(n\) clusters.
Fusion : On trouve les deux clusters les plus “proches” et on les fusionne en un seul. Nous avons maintenant \(n-1\) clusters.
Répétition : On répète l’étape de fusion jusqu’à ce qu’il ne reste plus qu’un seul grand cluster contenant toutes les données.

Ce processus crée une hiérarchie complète, un arbre de relations qui montre comment les points se regroupent à différents niveaux de similarité.

3 Le Cœur de l’Algorithme : Le Critère de Liaison (Linkage)

La question la plus importante est : comment mesurer la distance entre deux clusters (qui peuvent contenir plusieurs points) ? Le choix de cette mesure, appelée critère de liaison, détermine la forme des clusters que l’algorithme va trouver.

Single Linkage (Lien Simple) : La distance entre deux clusters est la distance entre leurs deux points les plus proches. Cette méthode a tendance à créer de longs “chaînages” et est sensible au bruit.
Complete Linkage (Lien Complet) : La distance est celle entre leurs deux points les plus éloignés. Elle a tendance à produire des clusters plus compacts et sphériques.
Average Linkage (Lien Moyen) : La distance est la moyenne de toutes les distances entre les paires de points des deux clusters. C’est un bon compromis entre les deux précédentes.
Ward’s Linkage (Lien de Ward) : C’est souvent le choix par défaut et le plus performant. L’idée est de fusionner les deux clusters qui entraînent la plus faible augmentation de la variance intra-cluster. Il cherche à créer les clusters les plus compacts et homogènes possible.

4 Le Dendrogramme : La Carte d’Identité du Clustering

Le résultat visuel du clustering hiérarchique est le dendrogramme. C’est un diagramme en arbre qui représente les fusions successives des clusters.

Comment le lire :

L’axe des x représente les observations individuelles.
L’axe des y représente la distance (ou dissimilarité). La hauteur d’une ligne horizontale indique la distance à laquelle deux clusters ont été fusionnés.
Plus une fusion se produit haut dans le dendrogramme, plus les deux clusters fusionnés sont dissimilaires.

Le dendrogramme est un outil de diagnostic fantastique. On peut choisir le nombre de clusters a posteriori en traçant une ligne horizontale. Le nombre de lignes verticales que cette ligne de coupe traverse correspond au nombre de clusters.

5 Atelier Pratique : Segmenter des Clients

Imaginons que nous ayons des données sur les clients d’un centre commercial : leur revenu annuel et un “score de dépense”. Nous voulons les segmenter pour des campagnes marketing.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import AgglomerativeClustering

# 1. Créer des données synthétiques de clients
np.random.seed(0)
# Utilisons un jeu de données connu pour cet exemple pour la reproductibilité
try:
    df = pd.read_csv('https://raw.githubusercontent.com/uiuc-cse/data-fa14/gh-pages/data/mall_customers.csv')
    df = df.rename(columns={'Annual Income (k$)': 'income', 'Spending Score (1-100)': 'score'})
    X = df[['income', 'score']]
except:
    print("Données de secours")
    from sklearn.datasets import make_blobs
    X, _ = make_blobs(n_samples=200, centers=5, cluster_std=1.2, random_state=42)
    X = pd.DataFrame(X, columns=['income', 'score'])


# 2. Mise à l'échelle des données
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. Générer la matrice de liaison et tracer le dendrogramme
# Nous utilisons la méthode de Ward pour une segmentation équilibrée
print("--- Génération du Dendrogramme avec la méthode de Ward ---")
linked = linkage(X_scaled, method='ward')

plt.figure(figsize=(15, 10))
dendrogram(linked,
            orientation='top',
            distance_sort='descending',
            show_leaf_counts=True)
plt.title('Dendrogramme du Clustering Hiérarchique')
plt.xlabel("Index des observations")
plt.ylabel("Distance (Ward)")
# On ajoute une ligne de coupe pour suggérer un nombre de clusters
plt.axhline(y=12, color='r', linestyle='--')
plt.show()
print("Le dendrogramme suggère qu'une coupe autour d'une distance de 12 (ligne rouge) donnerait 5 clusters, ce qui semble être un bon choix.\n")

# 4. Appliquer le clustering agglomératif avec le nombre de clusters choisi
# Nous choisissons K=5 en nous basant sur l'inspection du dendrogramme
k = 5
agg_cluster = AgglomerativeClustering(n_clusters=k, affinity='euclidean', linkage='ward')
labels = agg_cluster.fit_predict(X_scaled)

# 5. Visualiser les clusters finaux
plt.figure(figsize=(12, 8))
sns.scatterplot(x=X['income'], y=X['score'], hue=labels, palette=sns.color_palette('viridis', n_colors=k), s=100, alpha=0.8)
plt.title(f'Résultat du Clustering Hiérarchique (K={k})')
plt.xlabel('Revenu Annuel')
plt.ylabel('Score de Dépense')
plt.legend(title='Cluster')
plt.show()

6 Conclusion

Le clustering hiérarchique est une alternative très riche au K-Means.

Avantages :

Pas besoin de choisir K à l’avance. Le dendrogramme nous permet de faire ce choix de manière informée.
Très visuel. Le dendrogramme fournit une interprétation détaillée de la structure des données.
Peut révéler des relations de parenté et des structures imbriquées.

Inconvénients :

Coût de calcul élevé. Il ne s’adapte pas bien aux très grands jeux de données (la complexité est au moins \(O(n^2)\)).
Les fusions sont définitives. Une fois qu’un point est assigné à un groupe, il ne peut plus en sortir, ce qui peut conduire à des solutions sous-optimales.

Et maintenant ?

Nous avons vu des méthodes qui supposent des clusters sphériques (K-Means) ou qui construisent une hiérarchie (clustering agglomératif). Mais que faire si les clusters ont des formes étranges, comme des lunes ou des cercles concentriques, et qu’il y a du bruit ? Pour cela, nous devons changer de paradigme et penser en termes de densité. Ce sera l’objet de notre prochain article sur DBSCAN.