Formalisation de l’Apprentissage Supervisé : Du Risque à la Validation Croisée

1 Un Cadre pour l’Apprentissage

Dans notre précédent article, nous avons exploré le Machine Learning de manière intuitive. Nous allons maintenant mettre un cadre mathématique rigoureux sur ces concepts. Cette formalisation est essentielle pour comprendre en profondeur le “pourquoi” derrière les algorithmes et les méthodologies que nous utilisons.

En apprentissage supervisé, nous partons d’un jeu de données, ou échantillon, noté : \[D_n = \left\{(x_i, y_i)\right\}_{i=1}^n\]

Ce jeu de données est constitué de \(n\) paires d’observations. Pour chaque individu \(i\) :

• \(x_i \in \mathcal{X}\) est le vecteur des variables explicatives (ou features). \(\mathcal{X}\) est l’espace de ces variables, souvent \(\mathbb{R}^d\) où \(d\) est le nombre de features.
• \(y_i \in \mathcal{Y}\) est l’étiquette (ou label), c’est-à-dire la sortie que nous voulons prédire. \(\mathcal{Y}\) est l’espace des étiquettes.

On suppose que ces paires \((x_i, y_i)\) sont des réalisations de vecteurs aléatoires \((X, Y)\) suivant une distribution de probabilité jointe \(P(X, Y)\) qui nous est inconnue.

L’Objectif Fondamental

Le but de l’apprentissage supervisé est d’utiliser l’échantillon \(D_n\) pour apprendre une fonction \(f: \mathcal{X} \to \mathcal{Y}\), appelée prédicteur, qui est capable de prédire la bonne étiquette \(y\) pour une nouvelle entrée \(x\) non observée.

2 Le Prédicteur : Régresseur ou Classifieur ?

Le terme “prédicteur” est générique. Sa nature exacte dépend de la nature de l’espace des étiquettes \(\mathcal{Y}\).

2.1 Régresseur

Si l’étiquette \(y\) est une variable quantitative continue (ex: un prix, une température), alors \(\mathcal{Y} \subseteq \mathbb{R}\). Dans ce cas, le prédicteur \(f\) est appelé un régresseur. Le problème est un problème de régression.

2.2 Classifieur

Si l’étiquette \(y\) est une variable qualitative qui représente une catégorie, alors \(\mathcal{Y}\) est un ensemble fini de valeurs discrètes. Le prédicteur \(f\) est appelé un classifieur (ou classificateur). On distingue deux cas principaux :

• Classification Binaire : Il n’y a que deux classes possibles. Par convention, \(\mathcal{Y} = \{0, 1\}\) ou \(\mathcal{Y} = \{-1, 1\}\).

  • Exemples : Spam/Non-Spam, Malade/Sain, Client va résilier/Ne va pas résilier.

• Classification Multi-classes : Il y a \(K > 2\) classes possibles. \(\mathcal{Y} = \{c_1, c_2, \dots, c_K\}\).

  • Exemples : Reconnaissance de chiffres (10 classes de 0 à 9), classification d’articles de presse (Sport, Politique, Économie…).

3 Mesurer l’Erreur : La Fonction de Perte

Comment savoir si un prédicteur \(f\) est “bon” en un point donné ? Nous devons quantifier l’erreur qu’il commet. C’est le rôle de la fonction de perte (ou loss function), notée \(L\).

La fonction de perte \(L(y, \hat{y})\) mesure le “coût” de prédire \(\hat{y} = f(x)\) alors que la vraie valeur était \(y\).

Example 1 (Exemples de fonctions de perte standards)  

• Pour la Régression :

  • Erreur Quadratique (Squared Error) : \(L(y, \hat{y}) = (y - \hat{y})^2\). C’est la plus courante, elle pénalise fortement les grandes erreurs.
  • Erreur Absolue (Absolute Error) : \(L(y, \hat{y}) = |y - \hat{y}|\). Elle est plus robuste aux valeurs aberrantes (outliers).

• Pour la Classification :

  • Perte 0-1 (0-1 Loss) : \(L(y, \hat{y}) = \mathbb{I}(y \neq \hat{y})\), où \(\mathbb{I}(\cdot)\) est la fonction indicatrice (vaut 1 si la condition est vraie, 0 sinon). C’est la mesure la plus naturelle (l’erreur est de 1 si on se trompe, 0 sinon), mais elle est difficile à optimiser directement. C’est pourquoi on utilise souvent des fonctions de perte “surrogates” (ex: Hinge Loss, Log Loss).
  • Perte Charnière (Hinge Loss) : Utilisée principalement par les SVMs. Pour des étiquettes \(y \in \{-1, 1\}\), la perte est \(L(y, f(x)) = \max(0, 1 - y \cdot f(x))\). Elle pénalise les prédictions incorrectes et celles qui sont correctes mais pas assez “confiantes”.
  • Perte Logarithmique (Log Loss) ou Entropie Croisée : C’est la fonction de perte standard pour la régression logistique et les réseaux de neurones. Pour une classification binaire avec \(y \in \{0, 1\}\) et une prédiction probabiliste \(\hat{p} = P(Y=1|X=x)\), la perte est \(L(y, \hat{p}) = -[y \log(\hat{p}) + (1-y) \log(1-\hat{p})]\). Elle pénalise lourdement les prédictions qui sont à la fois fausses et très confiantes.

4 L’Objectif Idéal : Minimiser le Risque Vrai

4.1 Définition du Risque Vrai

Nous ne nous intéressons pas à l’erreur sur un seul point, mais à la performance moyenne de notre prédicteur sur toutes les données possibles. C’est le concept de risque.

Définition du Risque

Le risque vrai (ou espérance de la perte) d’un prédicteur \(f\) est défini par : \[R(f) = \mathbb{E}_{(X,Y) \sim P}[L(Y, f(X))]\] Le risque \(R(f)\) représente l’erreur moyenne que \(f\) commettrait sur une nouvelle observation \((X, Y)\) tirée de la distribution de probabilité \(P\).

Le Problème Fondamental du Machine Learning

• Le prédicteur idéal \(f^*\) est celui qui minimise ce risque vrai: \[f^* = \arg\min_{f \in \mathcal{F}} R(f)\]

• Cependant, nous ne pouvons pas calculer \(R(f)\) directement, car la distribution \(P(X, Y)\) nous est inconnue.

• Caractériser le prédicteur idéal peut aider à concevoir des méthodes ou algorithmes pour l’estimer à partir des données.

4.2 Régresseur Idéal pour le Risque Quadratique

Dans le cas de la régression avec la perte quadratique, on peut montrer que le prédicteur idéal \(f^*\) qui minimise le risque vrai \(R(f) = \mathbb{E}[(Y - f(X))^2]\) est la fonction d’espérance conditionnelle.

\[f^*(x) = \mathbb{E}[Y | X=x]\]

Intuition : Pour une nouvelle entrée \(x\) donnée, la meilleure prédiction possible (au sens de l’erreur quadratique moyenne) est la moyenne de toutes les valeurs de \(Y\) que l’on pourrait observer pour cette même entrée \(x\).

Tous les algorithmes de régression (régression linéaire, arbres de décision, réseaux de neurones…) sont en réalité des méthodes différentes pour essayer d’estimer cette fonction d’espérance conditionnelle \(\mathbb{E}[Y | X=x]\) à partir des données de l’échantillon \(D_n\).

4.3 Classifieur Idéal pour le Risque 0-1

Dans le cas de la classification avec la perte 0-1, le risque \(R(f) = \mathbb{E}[\mathbb{I}(Y \neq f(X))]\) est simplement la probabilité de mal classer une nouvelle observation.

Le prédicteur idéal \(f^*\) qui minimise ce risque est appelé le classifieur de Bayes. Il est défini par la règle suivante :

\[f^*(x) = \underset{c \in \mathcal{Y}}{\operatorname{argmax}} \mathbb{P}(Y=c | X=x)\]

Intuition : Pour une nouvelle entrée \(x\), la meilleure stratégie pour minimiser l’erreur est de prédire la classe \(c\) qui a la plus grande probabilité d’apparaître, sachant \(x\).

Tous les algorithmes de classification (régression logistique, SVM, arbres de décision…) sont des méthodes différentes pour essayer d’estimer ces probabilités conditionnelles \(P(Y=c | X=x)\) et d’approximer le classifieur de Bayes.

L’Erreur de Bayes : La Limite Infranchissable

Le risque du classifieur de Bayes, \(R(f^*)\), est appelé le risque de Bayes ou erreur de Bayes. C’est la plus petite erreur de classification possible. Elle n’est généralement pas nulle, car pour un même \(x\), il peut y avoir une incertitude sur la vraie classe \(y\) (chevauchement des distributions). C’est la limite théorique de performance pour un problème donné.

5 L’Approche Pratique : Minimiser le Risque Empirique

Puisque nous ne pouvons pas calculer le risque vrai, nous allons l’estimer en utilisant la seule chose que nous possédons : notre échantillon de données \(D_n\).

Le risque empirique est simplement la perte moyenne calculée sur notre jeu de données d’entraînement : \[ \hat{R}_n(f) = \frac{1}{n} \sum_{i=1}^{n} L(y_i, f(x_i)) \] La stratégie de base en ML, appelée Minimisation du Risque Empirique (ERM), consiste à choisir le prédicteur \(\hat{f}\) qui minimise ce risque empirique.

Cependant, cette approche a un danger majeur : le surapprentissage (overfitting). Un modèle peut devenir excellent pour mémoriser les données d’entraînement (risque empirique très faible) mais être incapable de généraliser à de nouvelles données (risque vrai élevé).

6 Estimer la Performance de Généralisation

Comment obtenir une estimation fiable de la performance de notre modèle sur de nouvelles données ? En ne testant jamais le modèle sur les données qu’il a utilisées pour apprendre !

6.1 La Méthode Hold-Out (Train/Test Split)

L’approche la plus simple est de diviser notre jeu de données \(D_n\) en deux :

1. Un jeu d’entraînement (Training Set) : utilisé pour entraîner le modèle (minimiser le risque empirique).
2. Un jeu de test (Test Set) : mis de côté et utilisé une seule fois à la fin pour estimer le risque vrai du modèle final.

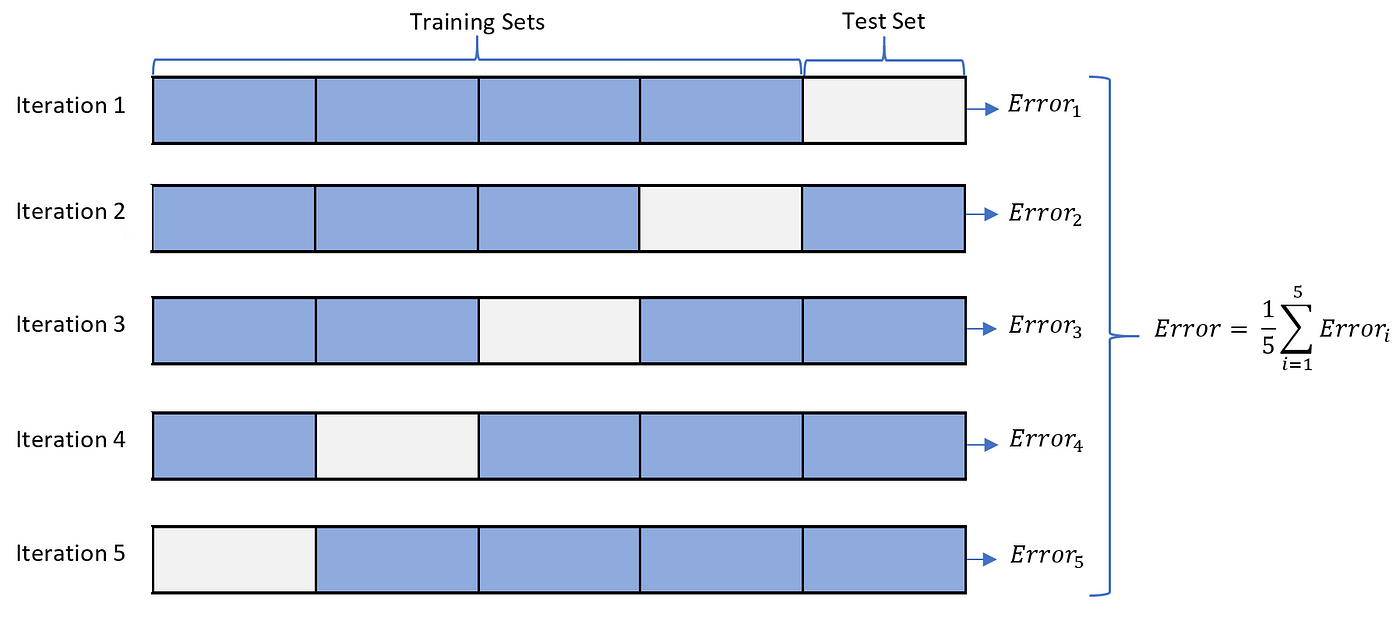
6.2 La Validation Croisée (Cross-Validation)

La méthode Hold-Out a un inconvénient : l’estimation de la performance peut dépendre fortement de la manière dont la division a été faite. Une méthode plus robuste et qui utilise mieux les données est la validation croisée à K-blocs (K-Fold Cross-Validation).

Le processus :

1. On divise aléatoirement le jeu de données d’entraînement en \(K\) sous-ensembles (ou “blocs”, folds) de taille égale.

2. On boucle \(K\) fois :

   • À chaque itération \(k\), on utilise le bloc \(k\) comme jeu de validation et les \(K-1\) autres blocs comme jeu d’entraînement.
   • On entraîne un modèle et on calcule sa performance sur le jeu de validation.

3. La performance finale du modèle est la moyenne des \(K\) performances obtenues.

Variantes notables :

• Leave-One-Out Cross-Validation (LOOCV) : Un cas extrême où \(K=n\). On entraîne \(n\) modèles en laissant une seule observation de côté à chaque fois. C’est très coûteux mais donne une estimation de l’erreur peu biaisée.
• Stratified K-Fold : Pour les problèmes de classification, cette variante s’assure que la proportion de chaque classe est la même dans chaque bloc, ce qui est crucial pour les jeux de données déséquilibrés.

7 Conclusion

Nous avons mis en place un cadre formel pour l’apprentissage supervisé. Nous avons vu que l’objectif est de trouver un prédicteur qui minimise une fonction de perte. Comme le risque vrai est inaccessible, nous minimisons le risque empirique, mais nous devons nous prémunir contre le surapprentissage. Pour cela, des techniques d’estimation robustes comme la validation croisée sont des outils indispensables pour évaluer honnêtement la capacité de nos modèles à généraliser à de nouvelles données.

8 Exercices

Exercise 1  

Question 1

Dans le cadre de l’apprentissage supervisé, que représente \(D_n = \{(x_i, y_i)\}_{i=1}^n\) ?

1. Un ensemble de données non étiquetées.
2. Un échantillon de \(n\) paires (variables explicatives, étiquette).
3. La fonction de prédiction à apprendre.
4. Le risque empirique du modèle.

Question 2

Quelle est la principale différence entre un problème de régression et un problème de classification ?

1. La régression utilise des données non étiquetées, la classification des données étiquetées.
2. La régression prédit une catégorie, la classification une valeur continue.
3. La régression prédit une valeur continue, la classification une catégorie.
4. Il n’y a pas de différence fondamentale, les termes sont interchangeables.

Question 3

Quel est le rôle de la fonction de perte (Loss Function) \(L(y, \hat{y})\) ?

1. Mesurer la complexité du modèle.
2. Mesurer le coût de l’erreur lorsque l’on prédit \(\hat{y}\) au lieu de la vraie valeur \(y\).
3. Estimer la probabilité de la classe la plus fréquente.
4. Diviser les données en ensembles d’entraînement et de test.

Question 4

Laquelle de ces fonctions de perte est la plus couramment utilisée pour la régression logistique et les réseaux de neurones en classification ?

1. L’erreur quadratique (Squared Error).
2. La perte 0-1 (0-1 Loss).
3. La perte charnière (Hinge Loss).
4. La perte logarithmique (Log Loss) ou Entropie Croisée.

Question 5

Qu’est-ce que le “risque vrai” (True Risk) \(R(f)\) d’un prédicteur \(f\) ?

1. L’erreur moyenne calculée sur le jeu de données d’entraînement.
2. L’erreur moyenne que le prédicteur commettrait sur de nouvelles données invisibles.
3. Le nombre de fois où le modèle se trompe sur le jeu de test.
4. La complexité de la fonction de prédiction \(f\).

Question 6

Pourquoi ne peut-on pas minimiser directement le risque vrai en pratique ?

1. Parce que le calcul est trop complexe pour les ordinateurs modernes.
2. Parce que la fonction de perte est inconnue.
3. Parce que la distribution de probabilité jointe \(P(X, Y)\) des données est inconnue.
4. Parce que le risque vrai est toujours égal à zéro.

Question 7

Pour un problème de régression, quel est le prédicteur idéal \(f^*(x)\) qui minimise le risque quadratique ?

1. La médiane conditionnelle, \(Median(Y | X=x)\).
2. La classe la plus probable, \(\operatorname{argmax}_c P(Y=c | X=x)\).
3. L’espérance conditionnelle, \(\mathbb{E}[Y | X=x]\).
4. Le mode conditionnel, \(Mode(Y | X=x)\).

Question 8

Le classifieur de Bayes, qui minimise le risque de classification 0-1, prédit…

1. La classe qui a la plus petite variance.
2. La classe qui a la plus grande probabilité conditionnelle \(P(Y=c | X=x)\).
3. Toujours la classe la plus fréquente dans le jeu de données.
4. La classe la plus proche dans l’espace des features.

Question 9

Quel est le principal danger de la stratégie de Minimisation du Risque Empirique (ERM) ?

1. Le sous-apprentissage (underfitting), où le modèle est trop simple.
2. Le surapprentissage (overfitting), où le modèle mémorise les données d’entraînement mais généralise mal.
3. La lenteur du calcul sur de grands jeux de données.
4. L’impossibilité de trouver un minimum pour le risque empirique.

Question 10

Quelle est la principale utilité de la validation croisée (K-Fold Cross-Validation) ?

1. Entraîner le modèle plus rapidement.
2. Obtenir une estimation plus robuste de la performance de généralisation du modèle que la simple division Entraînement/Test.
3. Augmenter la taille du jeu de données d’entraînement.
4. Sélectionner automatiquement la meilleure fonction de perte.