DBSCAN

Code

require(reticulate)

1 Introduction au Clustering et à DBSCAN

1.1 Qu’est-ce que le clustering ?

Le partitionnement de données, plus communément appelé clustering, est une tâche fondamentale de l’apprentissage non supervisé. Son objectif principal est d’explorer des ensembles de données pour lesquels nous ne disposons pas d’étiquettes préalables. Il s’agit de regrouper ces données en sous-ensembles homogènes, nommés clusters. Au sein de chaque cluster, les observations partagent des caractéristiques communes, tandis qu’elles se distinguent des observations des autres clusters.

Les applications du clustering sont nombreuses et variées :

Segmentation de marché : Identifier des groupes d’utilisateurs ou de clients ayant des comportements similaires.
Analyse de réseaux sociaux : Détecter des communautés.
Détection d’anomalies : Identifier des motifs récurrents inhabituels, par exemple dans des transactions financières.
Segmentation d’images : Regrouper les pixels appartenant à un même objet dans une image.
Bioinformatique : Identifier des patients dont la maladie s’explique par un même profil génétique.
Organisation de données : Par exemple, annoter automatiquement des corpus de documents en les regroupant par sujet, ce qui peut être moins coûteux et plus efficace qu’une annotation manuelle.

1.2 Pourquoi DBSCAN ?

Les algorithmes de clustering traditionnels, comme $K$-Means, montrent certaines limites. Ils peinent notamment à identifier des clusters qui ne sont pas de forme sphérique ou convexe et peuvent être fortement influencés par la présence de bruit ou de points aberrants dans les données. De plus, $K$-Means requiert de spécifier le nombre de clusters $K$ à l’avance.

C’est ici qu’intervient DBSCAN (Density-Based Spatial Clustering of Applications with Noise). Proposé en 1996 par Martin Ester, Hans-Peter Kriegel, Jörg Sander et Xiaowei Xu, cet algorithme offre une approche basée sur la densité pour partitionner les données. L’idée principale de DBSCAN est que pour qu’un point appartienne à un regroupement (cluster), il doit avoir un nombre suffisant de points voisins à proximité. Les points qui n’ont pas assez de voisins sont considérés comme du bruit.

Les avantages clés de DBSCAN sont :

Sa capacité à découvrir des clusters de formes arbitraires.
Sa gestion robuste du bruit et des outliers, qui sont explicitement identifiés et non forcés dans un cluster.
Il ne nécessite pas de spécifier le nombre de clusters à l’avance.

DBSCAN est un algorithme populaire, reconnu pour sa pertinence et sa robustesse, comme en témoigne sa distinction “test of time award” à la conférence KDD en 2014.

1.3 $K$-Means vs DBSCAN

$K$-Means

Code

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons, make_circles
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

Code

# --- Génération des données ---

# Option 1: Deux lunes entrelacées
X_moons, y_moons = make_moons(n_samples=300, noise=0.07, random_state=42)

# Option 2: Cercles concentriques (autre exemple où K-Means échoue)
# X_circles, y_circles = make_circles(n_samples=300, factor=0.5, noise=0.05, random_state=42)

# Nous utiliserons les lunes pour cet exemple
X = X_moons
y_true = y_moons # Gardons les vraies étiquettes pour la visualisation

# Mise à l'échelle des données (souvent une bonne pratique, bien que K-Means soit moins sensible
# à l'échelle que DBSCAN qui repose sur des distances absolues pour epsilon)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# --- Visualisation des données originales ---
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y_true, cmap='viridis', s=50, alpha=0.8)
plt.title('Données Originales (Forme d\'arcs/lunes)')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.grid(True, linestyle='--', alpha=0.7)

# --- Application de K-Means ---
# K-Means a besoin de connaître le nombre de clusters à l'avance.
# Dans ce cas, nous savons qu'il y a 2 clusters.
kmeans = KMeans(n_clusters=2, random_state=42, n_init='auto')
kmeans_clusters = kmeans.fit_predict(X_scaled)

# --- Visualisation des résultats de K-Means ---
plt.subplot(1, 2, 2)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=kmeans_clusters, cmap='viridis', s=50, alpha=0.8)
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X', label='Centroïdes K-Means')
plt.title('Clustering K-Means (K=2)')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()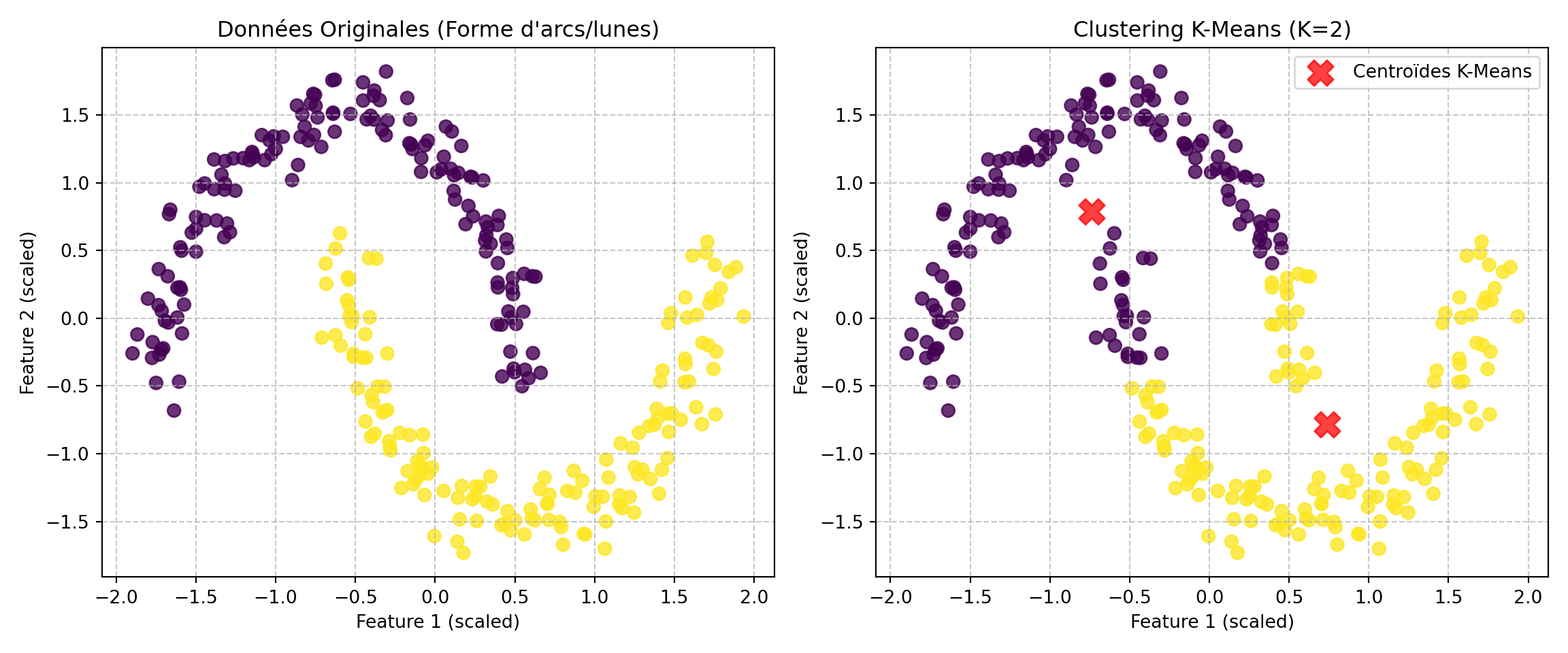

Explication des limites de K-Means sur ces données

K-Means tente de créer des clusters sphériques et de minimiser la somme des carrés des distances aux centroïdes.
Pour les données en forme de lunes, cette approche conduit à une séparation incorrecte des deux arcs car un seul centroïde ne peut pas bien représenter un arc de cercle.
Chaque cluster K-Means va ‘couper’ à travers les lunes plutôt que de les identifier comme des entités distinctes. C’est un scénario où un algorithme basé sur la densité comme DBSCAN serait plus approprié, car il peut identifier des régions denses de formes arbitraires.

Code

from sklearn.cluster import DBSCAN

# --- Application de DBSCAN ---
# DBSCAN nécessite deux paramètres principaux :
# 1. epsilon (eps): Le rayon autour d'un point. Si un point a au moins min_samples
#    points dans ce rayon, il est considéré comme un point central.
# 2. min_samples: Le nombre minimum de points dans le voisinage d'un point
#    (incluant le point lui-même) pour qu'il soit considéré comme un point central.

# Les valeurs optimales de eps et min_samples dépendent des données.
# Pour ces données en forme de lunes, on peut expérimenter.
# Une méthode courante pour estimer eps est d'utiliser la distance k-voisin le plus proche.
# Pour cet exemple, nous choisirons des valeurs qui fonctionnent bien visuellement.
dbscan = DBSCAN(eps=0.3, min_samples=5) # Ces valeurs peuvent nécessiter un ajustement
dbscan_clusters = dbscan.fit_predict(X_scaled)

# Les étiquettes de cluster produites par DBSCAN :
# Les points appartenant à un cluster auront une étiquette >= 0.
# Les points de bruit (outliers) auront l'étiquette -1.
unique_labels = np.unique(dbscan_clusters)
num_clusters = len(unique_labels) - (1 if -1 in unique_labels else 0)
num_noise_points = list(dbscan_clusters).count(-1)

print(f"\nRésultats de DBSCAN :")


Résultats de DBSCAN :

Code

print(f"Nombre de clusters détectés (sans compter le bruit) : {num_clusters}")

Nombre de clusters détectés (sans compter le bruit) : 2

Code

print(f"Nombre de points de bruit détectés : {num_noise_points}")

Nombre de points de bruit détectés : 0

Code

# --- Visualisation des résultats de DBSCAN ---
plt.figure(figsize=(6, 5))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=dbscan_clusters, cmap='viridis', s=50, alpha=0.8)
plt.title('Clustering DBSCAN')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()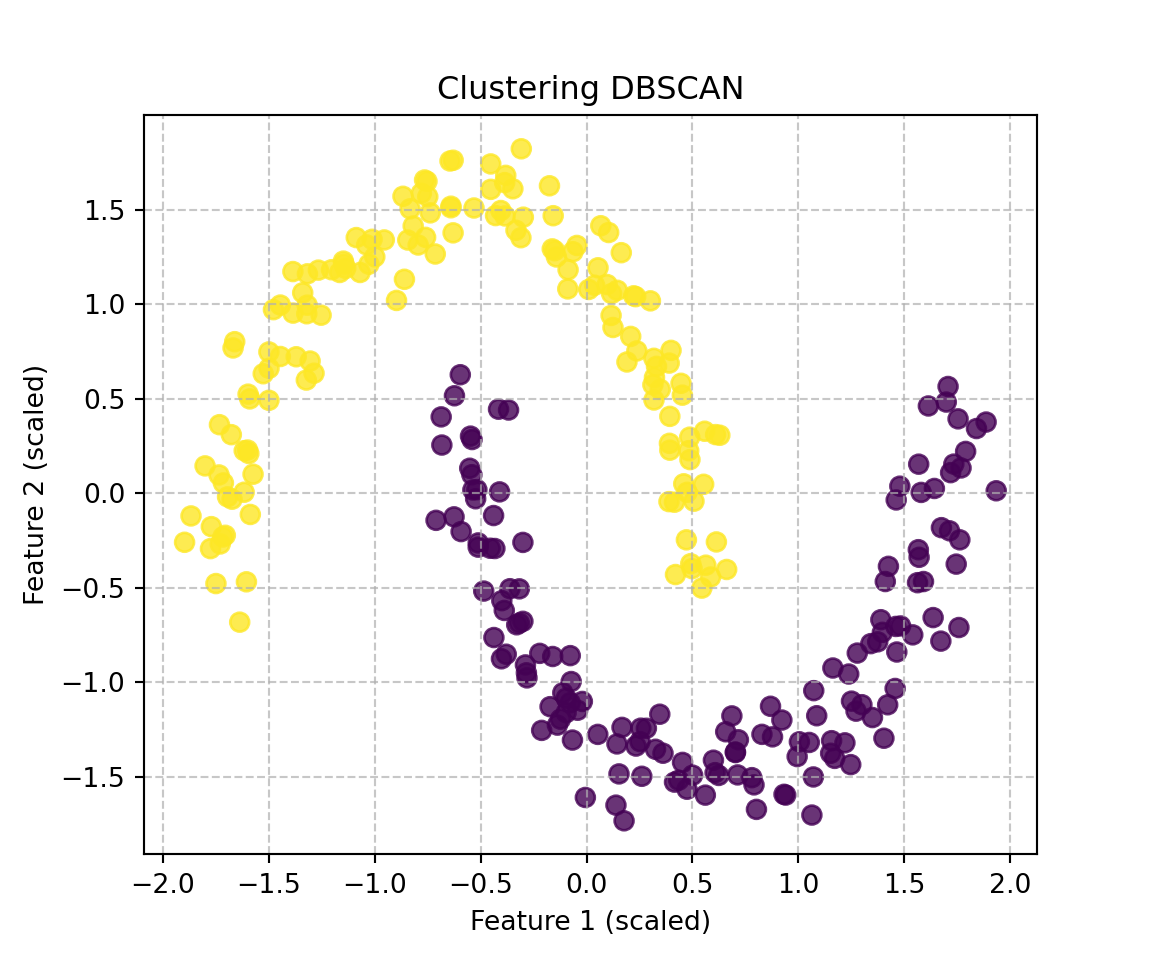

Explications sur ces données

DBSCAN a réussi à identifier les deux arcs comme des clusters distincts.
Il a attribué l’étiquette -1 aux points considérés comme du bruit (qui ne font partie d’aucune région dense).
L’efficacité de DBSCAN dépend fortement du choix des paramètres eps et min_samples.
- eps trop petit : peut diviser des clusters réels ou classer des points comme du bruit.
- eps trop grand : peut fusionner des clusters distincts.
- min_samples trop petit : peut identifier du bruit comme des clusters.
- min_samples trop grand : peut transformer des points de cluster en bruit.

2 Concepts fondamentaux

Soit un ensemble de données $\mathcal{D}_n = \{x_1, x_2, \ldots, x_n\}$, où $x_i \in \mathbb{R}^d$ pour un certain $d$. L’algorithme DBSCAN utilise deux paramètres :

$\epsilon \in \mathbb{R}^+$: Rayon du voisinage.
$\text{minPts} \in \mathbb{N}^+$: Nombre minimum de points dans un $\epsilon$-voisinage pour considérer un point comme un point central.

Notons $V_{\epsilon}(x_i)$ l’$\epsilon$-voisinage du point $x_i$, défini comme : \[V_{\epsilon}(x_i) = \{x_j \in \mathcal{D}_n \mid \text{dist}(x_i, x_j) \leq \epsilon \}\] où $\text{dist}(\cdot, \cdot)$ est une fonction de distance (par exemple, la distance Euclidienne). Le nombre de voisins de $x_i$ est $|V_{\epsilon}(x_i)|$.

2.1 Définitions Clés

Point Central (Core Point): Un point $x_i \in \mathcal{D}_n$ est un point central si son $\epsilon$-voisinage contient au moins $\text{minPts}$ points : \[|V_{\epsilon}(x_i)| \geq \text{minPts}\]
Directement Accessible par Densité (Directly Density-Reachable): Un point $x_j$ est directement accessible par densité depuis un point $x_i$ si :
1. $x_j \in V_{\epsilon}(x_i)$
2. $x_i$ est un point central (c.-à-d. $|V_{\epsilon}(x_i)| \geq \text{minPts}$)
Accessible par Densité (Density-Reachable): Un point $x_j$ est accessible par densité depuis un point $x_i$ (noté $x_i \leadsto x_j$) s’il existe une séquence de points $p_1, p_2, \ldots, p_k$ telle que :
1. $p_1 = x_i$ et $p_k = x_j$
2. $p_{m+1}$ est directement accessible par densité depuis $p_m$ pour $1 \leq m < k$. Cela implique que $p_1, \ldots, p_{k-1}$ doivent être des points centraux. $p_k$ peut être un point central ou un point frontière.
Connecté par Densité (Density-Connected): Deux points $x_i$ et $x_j$ sont connectés par densité s’il existe un point $x_k \in \mathcal{D}_n$ tel que $x_k$ est un point central, et $x_i$ et $x_j$ sont tous deux accessibles par densité depuis $x_k$. \[\exists x_k \in \mathcal{D}_n \text{ t.q. } |V_{\epsilon}(x_k)| \geq \text{minPts} \text{ et } (x_k \leadsto x_i) \text{ et } (x_k \leadsto x_j)\]
Point Frontière (Border Point): Un point $x_i$ est un point frontière s’il n’est pas un point central, mais il est accessible par densité depuis un point central $x_c$. \[ (|V_{\epsilon}(x_i)| < \text{minPts}) \land (\exists x_c \in \mathcal{D}_n \text{ t.q. } (|V_{\epsilon}(x_c)| \geq \text{minPts}) \land (x_c \leadsto x_i)) \] Plus simplement, un point $x_i$ est un point frontière s’il n’est pas un point central, mais $x_i \in V_{\epsilon}(x_c)$ pour un certain point central $x_c$.
Point Aberrant (Noise Point / Outlier): Un point $x_i$ est un point aberrant s’il n’est ni un point central, ni un point frontière. C’est-à-dire qu’il n’est accessible par densité depuis aucun point central. \[\forall x_c \in \mathcal{D}_n \text{ t.q. } |V_{\epsilon}(x_c)| \geq \text{minPts}, \text{ on a } \neg (x_c \leadsto x_i)\]

2.2 Structure d’un Cluster

Un cluster $C$ dans DBSCAN est un sous-ensemble non vide de $\mathcal{D}_n$ satisfaisant deux propriétés :

Maximalité: Pour tout $x_i, x_j \in \mathcal{D}_n$, si $x_i \in C$ et $x_j$ est accessible par densité depuis $x_i$, alors $x_j \in C$.
Connectivité: Pour tout $x_i, x_j \in C$, $x_i$ et $x_j$ sont connectés par densité.

3 L’Algorithme DBSCAN Étape par Étape ⚙️

3.1 Algorithme Détaillé

Entrées:

$\mathcal{D}_n$: un ensemble de $n$ points de données $\{x_1, \dots, x_n\}$.
$\epsilon$: le rayon du voisinage.
$\text{minPts}$: le nombre minimum de points dans un $\epsilon$-voisinage.

Sorties:

Un ensemble d’assignations de cluster cluster_id[1...n] où cluster_id[i] est l’identifiant du cluster pour $x_i$, ou une valeur spéciale pour le bruit (par exemple, NOISE).

Variables internes:

visited[1...n]: tableau de booléens, initialisé à false.
cluster_id[1...n]: tableau d’entiers, initialisé à UNCLASSIFIED (ou 0).
current_cluster_id: entier, initialisé à 0.

Constantes symboliques (exemples):

UNCLASSIFIED = 0
NOISE = -1

Procédure DBSCAN($\mathcal{D}_n, \epsilon, \text{minPts}$):

Pour $i$ de $1$ à $n$:
1. Si visited[i] est true, passer au point suivant.
2. Marquer visited[i] = true.
3. $Neighbors_i = RegionQuery(x_i, \epsilon, \mathcal{D}_n)$ .
4. Si $|Neighbors_i| < \text{minPts}$:
  1. Marquer cluster_id[i] = NOISE.
5. Sinon ($x_i$ est un point central):
  1. current_cluster_id = current_cluster_id + 1.
  2. ExpandCluster(x_i, Neighbors_i, current_cluster_id, \epsilon, \text{minPts}, \mathcal{D}_n, visited, cluster_id).

Procédure auxiliaire ExpandCluster($P, Neighbors_P, C_{id}, \epsilon, \text{minPts}, \mathcal{D}_n, visited, cluster_id$):

Assigner cluster_id[index_of(P)] = C_{id}. (Assurer que le point $P$ initial est bien dans le cluster)
Initialiser une file (ou une pile) S avec tous les points de Neighbors_P.
Tant que S n’est pas vide:
1. Prendre un point $Q$ de S (et le retirer de S).
2. Si visited[index_of(Q)] est false:
  1. Marquer visited[index_of(Q)] = true.
  2. Neighbors_Q = RegionQuery(Q, \epsilon, \mathcal{D}_n).
  3. Si $|Neighbors_Q| \geq \text{minPts}$ ($Q$ est aussi un point central): Pour chaque point $R$ dans Neighbors_Q: Si cluster_id[index_of(R)] est UNCLASSIFIED ou NOISE: Ajouter $R$ à S (si pas déjà présent, géré par la structure de données de S ou par un test explicite).
3. Si cluster_id[index_of(Q)] est UNCLASSIFIED ou NOISE:
  1. Assigner cluster_id[index_of(Q)] = C_{id}.

Procédure auxiliaire RegionQuery($P, \epsilon, \mathcal{D}_n$):

Retourner l’ensemble $\{X \in \mathcal{D}_n \mid \text{dist}(P, X) \leq \epsilon \}$.

Fin de l’algorithme: Une fois toutes les itérations de la boucle principale de DBSCAN terminées, le tableau cluster_id contient les assignations. Les points avec cluster_id[i] = NOISE sont des points aberrants. Les points avec cluster_id[i] > 0 appartiennent au cluster correspondant à leur ID.

Cette structure sépare la logique de balayage initial des points de la logique d’expansion d’un cluster une fois qu’un point central est trouvé. C’est une façon courante de décrire DBSCAN.

4 Choix des Paramètres `eps` et `minPts` pour DBSCAN ⚙️

Le choix des paramètres eps ($\epsilon$) et minPts est crucial pour la performance de l’algorithme DBSCAN et peut s’avérer non trivial. Il n’existe pas de méthode universelle, mais voici quelques approches et considérations :

4.1 Choix de `minPts`

Règle générale: minPts est souvent choisi en fonction de la dimensionnalité des données ($D$). Une règle empirique courante est de fixer minPts ≥ D + 1. Pour des données en 2 dimensions, un minPts de 3 ou 4 est un point de départ fréquent. Un minPts = 1 signifierait que chaque point est un cluster, et minPts = 2 est similaire à un clustering hiérarchique avec un critère de distance unique.
Robustesse au bruit: Des valeurs plus élevées de minPts tendent à produire des clusters plus denses et sont plus robustes au bruit (c’est-à-dire que plus de points seront classés comme bruit). Si les données sont très bruitées, augmenter minPts peut être bénéfique.
Connaissance du domaine: Si vous avez une attente sur la taille minimale des regroupements significatifs dans vos données, cela peut guider le choix de minPts.

4.2 Choix de `eps` ($\epsilon$)

Le choix de eps est souvent plus délicat et a un impact majeur sur les résultats.

Méthode du k-distance graph (ou coude/knee method):
1. Choisir une valeur pour minPts (par exemple, celle déterminée ci-dessus).
2. Pour chaque point de l’ensemble de données, calculer la distance à son $k$-ième plus proche voisin, où $k = \text{minPts} - 1$ (ou parfois $k = \text{minPts}$). Cette distance est appelée $k$-distance.
3. Trier ces $k$-distances par ordre croissant et les tracer.
4. Rechercher un “coude” (ou “knee”) dans le graphique. Ce point représente un seuil où les distances commencent à augmenter de manière significative. La valeur de distance à ce coude peut être un bon candidat pour eps. L’idée est que les points appartenant à un cluster auront leurs $k$-voisins relativement proches, tandis que les points de bruit ou les points à la frontière de régions moins denses auront des $k$-distances plus élevées.
Normalisation des données: Si les variables ont des échelles très différentes, il est recommandé de les normaliser (par exemple, Z-score) avant de calculer les distances, afin que eps ait une signification comparable pour toutes les dimensions.
Connaissance du domaine: Si l’échelle des distances attendues entre les points d’un même groupe est connue, cela peut aider à choisir eps.

4.3 Interaction entre `eps` et `minPts`

Ces deux paramètres sont interdépendants.

Si minPts est élevé, eps doit généralement être choisi plus grand pour s’assurer que des régions suffisamment denses puissent être trouvées.
Inversement, un minPts faible pourrait nécessiter un eps plus petit pour éviter de fusionner des clusters distincts ou d’inclure trop de bruit dans les clusters.

4.4 Approche Itérative et Évaluation

Expérimentation: Il est souvent nécessaire d’expérimenter avec différentes combinaisons de eps et minPts.
Inspection visuelle: Pour les données de faible dimension (2D ou 3D), la visualisation des clusters résultants peut grandement aider à évaluer la pertinence des paramètres.
Métriques de validation de clustering: Bien que DBSCAN ne vise pas à optimiser des métriques comme le coefficient de Silhouette (qui favorise les clusters convexes), ces métriques peuvent parfois donner une indication, surtout si on les compare sur différentes exécutions. Cependant, leur utilité est limitée pour les clusters de formes arbitraires trouvés par DBSCAN.
Stabilité: Rechercher des plages de valeurs pour eps et minPts où les résultats du clustering sont relativement stables.

4.5 Considérations pour des Densités Variables

DBSCAN utilise des paramètres globaux eps et minPts, ce qui peut poser problème si les données contiennent des clusters de densités très différentes. Dans de tels cas, des algorithmes plus avancés comme OPTICS ou HDBSCAN, qui peuvent identifier des clusters avec des densités variables, pourraient être plus appropriés.

En résumé, le choix des paramètres pour DBSCAN est un processus qui combine souvent des heuristiques, des analyses exploratoires (comme le k-distance graph) et une certaine part d’itération et d’évaluation en fonction du problème spécifique et des données.

4.6 La Métrique de Distance

Bien que ce ne soit pas un paramètre numérique au même titre que $\epsilon$ et minPts, le choix de la fonction de distance $d(x, y)$ est fondamental car il détermine comment la “proximité” est mesurée.

Distance Euclidienne : C’est le choix le plus courant pour des données numériques continues.
Autres distances : Pour des données spécifiques (e.g., textuelles, catégorielles, géospatiales), d’autres métriques comme la distance de Manhattan, la similarité cosinus (transformée en distance), la distance de Jaccard, ou des distances géodésiques peuvent être plus appropriées. Le choix de la distance doit refléter la notion de similarité pertinente pour le problème traité.

DBSCAN peut être rendu difficile à appliquer en très grande dimension à cause du “fléau de la dimension”, car les voisinages-$\epsilon$ ont tendance à ne contenir que leur centre. De plus, sa capacité à trouver des clusters de densités différentes est limitée par un choix unique de ε et minPts.

5 Avantages et Inconvénients de DBSCAN ⚖️

DBSCAN est un algorithme de clustering puissant et largement utilisé, mais comme toute technique, il présente des avantages et des inconvénients qu’il est important de considérer en fonction du contexte d’application.

5.1 Avantages de DBSCAN

Découverte de clusters de formes arbitraires : Contrairement à des algorithmes comme K-Means qui tendent à former des clusters sphériques, DBSCAN peut identifier des regroupements de données aux formes complexes et non convexes[. Il se base sur la notion de densité pour connecter les points.
Gestion robuste du bruit et des outliers : DBSCAN n’oblige pas tous les points à appartenir à un cluster. Il identifie explicitement les points qui se trouvent dans des régions de faible densité comme du bruit ou des outliers. Cela est particulièrement utile pour nettoyer des données ou détecter des anomalies.
Pas besoin de spécifier le nombre de clusters à l’avance : L’algorithme détermine automatiquement le nombre de clusters en fonction des paramètres de densité (ε et minPts) et de la structure des données.
Efficacité relative sur de grandes bases de données : Bien que la complexité puisse varier, DBSCAN peut être efficace en temps de calcul, notamment si des structures d’indexation spatiale sont utilisées pour accélérer la recherche des voisinages.

5.2 Inconvénients de DBSCAN

Difficulté avec les clusters de densités variables : DBSCAN utilise un seuil de densité global (défini par ε et minPts). Il peut donc avoir du mal à identifier correctement des clusters qui ont des densités internes très différentes. Un ensemble de paramètres qui fonctionne bien pour un cluster dense pourrait fusionner des clusters moins denses ou les marquer comme du bruit.
Sensibilité aux paramètres ε et minPts : Le choix de ε et minPts est crucial et peut significativement impacter les résultats du clustering. Trouver les bonnes valeurs nécessite souvent une certaine expertise, des tests itératifs ou des méthodes heuristiques.
Problèmes en haute dimension (Fléau de la dimension) : Dans les espaces de très grande dimension, la notion de distance et de densité peut devenir moins significative. Tous les points peuvent sembler éloignés les uns des autres, rendant difficile la définition d’un voisinage-ε pertinent et la formation de clusters denses. Les voisinages-ε ont tendance à ne contenir que leur centre en très grande dimension.
Dépendance à la métrique de distance : La qualité du clustering dépend de la pertinence de la métrique de distance utilisée pour la nature spécifique des données.

En résumé, DBSCAN est un excellent choix pour des données contenant du bruit et des clusters de formes non globulaires, à condition que les densités des clusters ne soient pas trop hétérogènes et que les paramètres soient bien ajustés.

6 Évaluation des Résultats de DBSCAN 📊

Une fois que DBSCAN (ou tout autre algorithme de clustering) a partitionné les données, il est crucial d’évaluer la qualité des clusters obtenus. Le clustering étant non supervisé, l’évaluation est plus délicate que pour les tâches d’apprentissage supervisé. On distingue généralement deux approches : l’évaluation interne, qui ne repose que sur les données et les clusters formés, et l’évaluation externe, qui compare les clusters à une vérité terrain (si disponible).

6.1 Évaluation Interne (sans vérité terrain)

Ces méthodes évaluent la qualité du clustering en se basant sur des propriétés intrinsèques des données et de la partition. L’idée générale est de quantifier à quel point les observations au sein d’un même cluster sont similaires (cohésion ou homogénéité) et à quel point les clusters distincts sont bien séparés (séparabilité).

Homogénéité (Compacité / Tightness)

L’homogénéité d’un cluster $C_k$ mesure à quel point ses membres sont proches les uns des autres, souvent en calculant la distance moyenne des observations au centroïde $\vec{\mu}_k$ du cluster. L’homogénéité du cluster $C_k$, notée $T_k$, est définie comme :

\[T_k = \dfrac{1}{|C_k|} \sum_{\vec{x} \in C_k} d(\vec{x}, \vec{\mu}_k)\]

où $|C_k|$ est le nombre de points dans le cluster $C_k$, et $\vec{\mu}_k = \dfrac{1}{|C_k|} \sum_{\vec{x} \in C_k} \vec{x}$ est le centroïde du cluster $C_k$. L’homogénéité globale $T$ du clustering est la moyenne des homogénéités des clusters:

\[T = \frac{1}{K} \sum_{k=1}^{K} T_k\]

Une faible valeur de $T_k$ (et donc de $T$) indique des clusters plus compacts et homogènes.

Séparabilité

La séparabilité quantifie à quel point les clusters sont distincts les uns des autres, typiquement en mesurant la distance entre leurs centroïdes. La séparabilité entre deux clusters $C_k$ et $C_l$, notée $S_{kl}$, est :

\[S_{kl} = d(\vec{\mu}_k, \vec{\mu}_l)\]

La séparabilité globale $S$ d’un clustering peut être la moyenne des séparabilités des paires de clusters:

\[S = \frac{2}{K(K-1)} \sum_{k=1}^{K-1} \sum_{l=k+1}^{K} S_{kl}\]

Une valeur élevée de $S_{kl}$ (et donc de $S$) est souhaitable.

Indice de Davies-Bouldin

Cet indice combine les notions d’homogénéité et de séparabilité. Pour chaque cluster $C_k$, on calcule $D_k$ en trouvant le cluster $C_l$ qui est le “moins bien séparé” par rapport à sa propre compacité et à celle de $C_k$:

\[D_k = \max_{l \neq k} \left( \frac{T_k + T_l}{S_{kl}} \right)\]

L’indice de Davies-Bouldin global $D$ est la moyenne des $D_k$:

\[D = \frac{1}{K} \sum_{k=1}^{K} D_k\]

Un indice de Davies-Bouldin plus faible indique un meilleur partitionnement, car cela signifie que les clusters sont plus compacts et mieux séparés.

Coefficient de Silhouette

Le coefficient de silhouette mesure pour chaque observation $\vec{x}$ à quel point elle est bien assignée à son cluster actuel, par rapport aux autres clusters. Il est défini comme :

\[s(\vec{x}) = \dfrac{b(\vec{x}) - a(\vec{x})}{\max(a(\vec{x}), b(\vec{x}))}\]

où : * $a(\vec{x})$ est la distance moyenne de $\vec{x}$ à tous les autres points du cluster auquel il appartient ($C_{k(\vec{x})}$): \[a(\vec{x}) = \frac{1}{|C_{k(\vec{x})}| - 1} \sum_{\vec{u} \in C_{k(\vec{x})}, \vec{u} \neq \vec{x}} d(\vec{u}, \vec{x})\] * $b(\vec{x})$ est la plus petite distance moyenne de $\vec{x}$ aux points d’un autre cluster (le cluster “voisin” le plus proche pour $\vec{x}$): \[b(\vec{x}) = \min_{l \neq k(\vec{x})} \left( \frac{1}{|C_l|} \sum_{\vec{u} \in C_l} d(\vec{u}, \vec{x}) \right)\]

Le coefficient $s(\vec{x})$ varie de -1 à 1:

Une valeur proche de +1 indique que $\vec{x}$ est bien assigné à son cluster et loin des clusters voisins.
Une valeur proche de 0 indique que $\vec{x}$ est proche de la frontière entre deux clusters.
Une valeur proche de -1 indique que $\vec{x}$ pourrait être mal assigné.

Le coefficient de silhouette global du clustering est la moyenne des $s(\vec{x})$ pour toutes les observations.

Stabilité des Clusters

Un autre critère qualitatif important est la stabilité des clusters. On s’attend à obtenir des résultats de clustering similaires si l’on perturbe légèrement les données (par exemple, en supprimant quelques observations) ou en modifiant l’ordre des données traitées par l’algorithme (DBSCAN peut y être sensible pour les points frontières). Une grande variabilité peut indiquer un mauvais choix de paramètres ou une structure de cluster peu fiable.

6.2 Évaluation Externe (avec vérité terrain)

Si l’on dispose d’étiquettes de classe réelles pour les données (vérité terrain), par exemple dans un cadre académique ou si des données partiellement étiquetées existent, on peut évaluer la concordance entre la partition trouvée par DBSCAN et ces classes réelles.

Indice de Rand

L’indice de Rand mesure la similarité entre deux partitionnements en considérant toutes les paires d’échantillons et en comptant les paires qui sont assignées de la même manière ou différemment dans les deux partitionnements. Soit $k(\vec{x}_i)$ le cluster assigné à $\vec{x}_i$ par DBSCAN et $y_i$ sa vraie classe. L’indice de Rand (RI) est:

\[RI = \frac{TP + TN}{TP + TN + FP + FN}\]

où, en considérant les paires de points :

$TP$ : nombre de paires de points qui sont dans la même vraie classe ET dans le même cluster.
$TN$ : nombre de paires de points qui sont dans des vraies classes différentes ET dans des clusters différents.
$FP$ : nombre de paires de points qui sont dans des vraies classes différentes MAIS dans le même cluster.
$FN$ : nombre de paires de points qui sont dans la même vraie classe MAIS dans des clusters différents.

Une formulation équivalente donnée dans le document est:

\[RI = \dfrac{2}{n(n-1)} \sum_{i=1}^{n-1} \sum_{l=i+1}^{n} (\mathbb{I}(k(\vec{x}_i) = k(\vec{x}_l)) \cdot \mathbb{I}(y_i = y_l) + \mathbb{I}(k(\vec{x}_i) \neq k(\vec{x}_l)) \cdot \mathbb{I}(y_i \neq y_l))\]

où $\mathbb{I}(\cdot)$ est la fonction indicatrice. L’indice de Rand varie entre 0 et 1, où 1 signifie une concordance parfaite. Il existe des versions ajustées (Adjusted Rand Index - ARI) qui corrigent l’effet du hasard.

D’autres métriques externes courantes incluent l’Information Mutuelle (et ses versions normalisées comme NMI) et les mesures basées sur la pureté, l’homogénéité et la complétude (différentes de l’homogénéité interne).

7 Implémentation Pratique de MyDBSCAN et Test 💻

Pour mieux comprendre le fonctionnement interne de DBSCAN, nous allons proposer une implémentation simple sous forme d’une classe Python MyDBSCAN. Ensuite, nous la testerons sur les données en forme de “lunes” que nous avons simulées précédemment pour illustrer les limites de K-Means.

Note

Cette implémentation est à des fins pédagogiques et se concentre sur la clarté de l’algorithme. Les bibliothèques comme scikit-learn offrent des versions optimisées de DBSCAN qui utilisent des structures de données avancées (comme les arbres KD ou les arbres Ball) pour une recherche de voisins plus efficace, ce qui les rend plus performantes sur de grands ensembles de données.

7.1 Notre implémentation

Code

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler

Code



class MyDBSCAN:
    def __init__(self, eps=0.5, min_pts=5):
        self.eps = eps
        self.min_pts = min_pts
        self.cluster_labels = None # Pour stocker l'étiquette de cluster de chaque point
        self.n_clusters_ = 0

    def _euclidean_distance(self, point1, point2):
        return np.sqrt(np.sum((point1 - point2)**2))

    def _region_query(self, X, point_idx):
        """Trouve tous les points dans le voisinage-eps du point_idx."""
        neighbors = []
        center_point = X[point_idx]
        for i, candidate_point in enumerate(X):
            if self._euclidean_distance(center_point, candidate_point) < self.eps:
                neighbors.append(i)
        return neighbors

    def _expand_cluster(self, X, point_idx, neighbors, cluster_id, visited_points):
        """Étend un cluster à partir d'un point noyau."""
        self.cluster_labels[point_idx] = cluster_id

        i = 0
        while i < len(neighbors):
            current_neighbor_idx = neighbors[i]

            if not visited_points[current_neighbor_idx]:
                visited_points[current_neighbor_idx] = True

                # Trouve les voisins du voisin actuel
                new_neighbors = self._region_query(X, current_neighbor_idx)

                if len(new_neighbors) >= self.min_pts:
                    # Si le voisin est aussi un point noyau, ajoute ses voisins à la liste
                    for nn_idx in new_neighbors:
                        if nn_idx not in neighbors: # Évite les doublons et les cycles infinis simples
                            neighbors.append(nn_idx)

            # Si le voisin n'est pas encore assigné à un cluster ou est marqué comme bruit (-1)
            if self.cluster_labels[current_neighbor_idx] == 0 or \
               self.cluster_labels[current_neighbor_idx] == -1:
                self.cluster_labels[current_neighbor_idx] = cluster_id

            i += 1

    def fit_predict(self, X):
        """Applique l'algorithme DBSCAN sur les données X."""
        n_points = X.shape[0]
        self.cluster_labels = np.zeros(n_points, dtype=int) # 0: non classifié, -1: bruit, >0: cluster_id
        visited_points = np.zeros(n_points, dtype=bool)
        cluster_id_counter = 0

        for i in range(n_points):
            if visited_points[i]:
                continue # Point déjà visité

            visited_points[i] = True
            neighbors = self._region_query(X, i)

            if len(neighbors) < self.min_pts:
                # Marquer comme bruit (peut être changé plus tard si point frontière)
                self.cluster_labels[i] = -1
            else:
                # Point noyau, démarrer un nouveau cluster
                cluster_id_counter += 1
                self._expand_cluster(X, i, neighbors, cluster_id_counter, visited_points)

        self.n_clusters_ = cluster_id_counter
        return self.cluster_labels

7.2 Test sur données simulées

Code

# --- Génération des données (identique à la section précédente) ---
X_moons, y_true_moons = make_moons(n_samples=300, noise=0.07, random_state=42)
scaler = StandardScaler()
X_moons_scaled = scaler.fit_transform(X_moons)

# --- Visualisation des données originales ---
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(X_moons[:, 0], X_moons[:, 1], c=y_true, cmap='viridis', s=50, alpha=0.8)
plt.title('Données Originales (Forme d\'arcs/lunes)')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.grid(True, linestyle='--', alpha=0.7)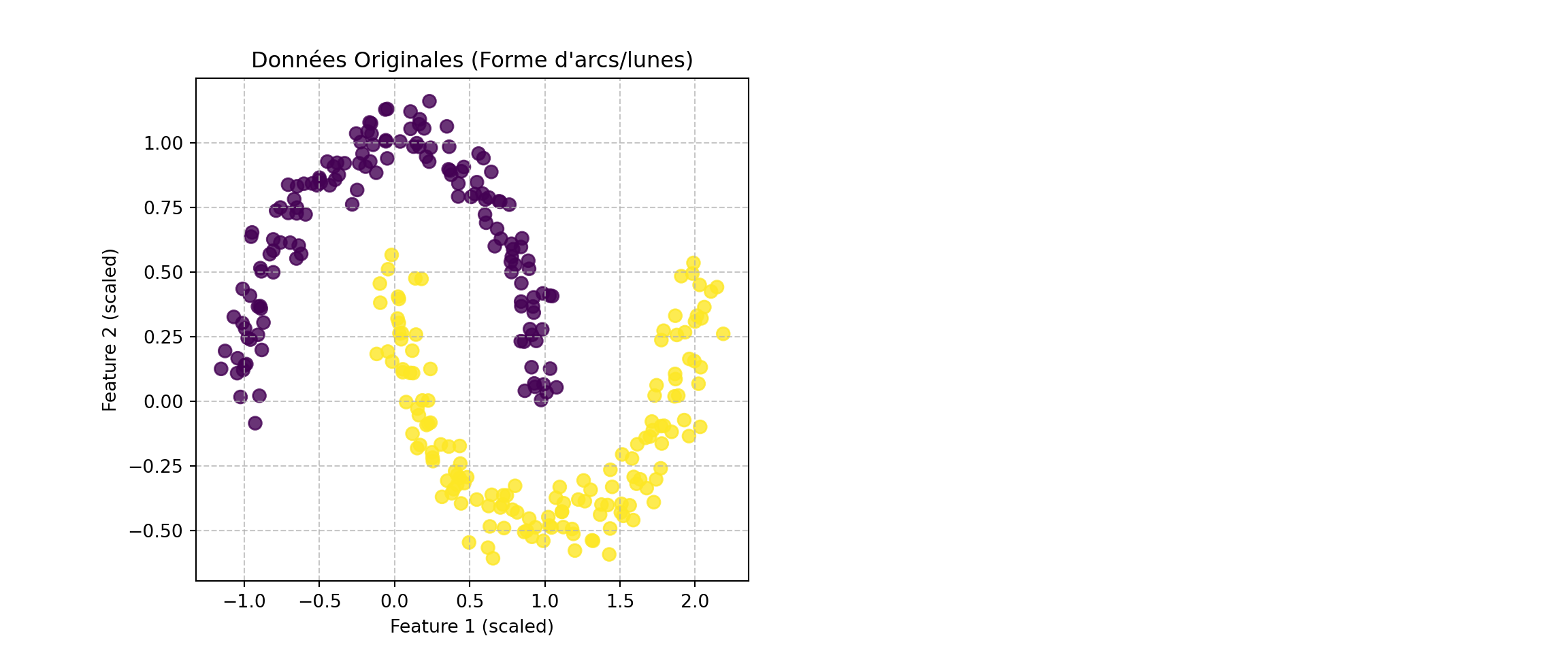

Code

# --- Test de MyDBSCAN ---
print("Test de MyDBSCAN sur les données 'lunes':")

Test de MyDBSCAN sur les données 'lunes':

Code

# Choix des paramètres pour MyDBSCAN (peuvent nécessiter un ajustement)
# Les valeurs de scikit-learn (eps=0.3, min_samples=5) étaient sur des données normalisées
# avec une implémentation optimisée. Nous pourrions avoir besoin d'ajuster.
# Commençons avec des valeurs similaires.
my_dbscan_custom = MyDBSCAN(eps=0.3, min_pts=5) # eps=0.3 semble un peu petit pour une implémentation simple
                                             # si les distances sont légèrement différentes.
                                             # Essayons eps=0.4 ou 0.5 si 0.3 ne donne rien de bon.
my_dbscan_custom_eps03_mp5 = MyDBSCAN(eps=0.3, min_pts=5)
clusters_custom_03_5 = my_dbscan_custom_eps03_mp5.fit_predict(X_moons_scaled)

my_dbscan_custom_eps04_mp5 = MyDBSCAN(eps=0.4, min_pts=5)
clusters_custom_04_5 = my_dbscan_custom_eps04_mp5.fit_predict(X_moons_scaled)


# --- Visualisation des résultats de MyDBSCAN ---
plt.figure(figsize=(18, 6))

# Graphique pour eps=0.3, min_pts=5
plt.subplot(1, 2, 1)
unique_labels_03_5 = np.unique(clusters_custom_03_5)
colors_03_5 = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels_03_5))]

for k, col in zip(unique_labels_03_5, colors_03_5):
    if k == -1: # Bruit
        col = [0, 0, 0, 1] # Noir

    class_member_mask = (clusters_custom_03_5 == k)
    xy = X_moons_scaled[class_member_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=7,
             label=f'Cluster {k}' if k != -1 else 'Bruit')

plt.title(f'MyDBSCAN (eps={my_dbscan_custom_eps03_mp5.eps}, min_pts={my_dbscan_custom_eps03_mp5.min_pts})')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)

# Graphique pour eps=0.4, min_pts=5
plt.subplot(1, 2, 2)
unique_labels_04_5 = np.unique(clusters_custom_04_5)
colors_04_5 = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels_04_5))]

for k, col in zip(unique_labels_04_5, colors_04_5):
    if k == -1: # Bruit
        col = [0, 0, 0, 1] # Noir

    class_member_mask = (clusters_custom_04_5 == k)
    xy = X_moons_scaled[class_member_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=7,
             label=f'Cluster {k}' if k != -1 else 'Bruit')

plt.title(f'MyDBSCAN (eps={my_dbscan_custom_eps04_mp5.eps}, min_pts={my_dbscan_custom_eps04_mp5.min_pts})')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()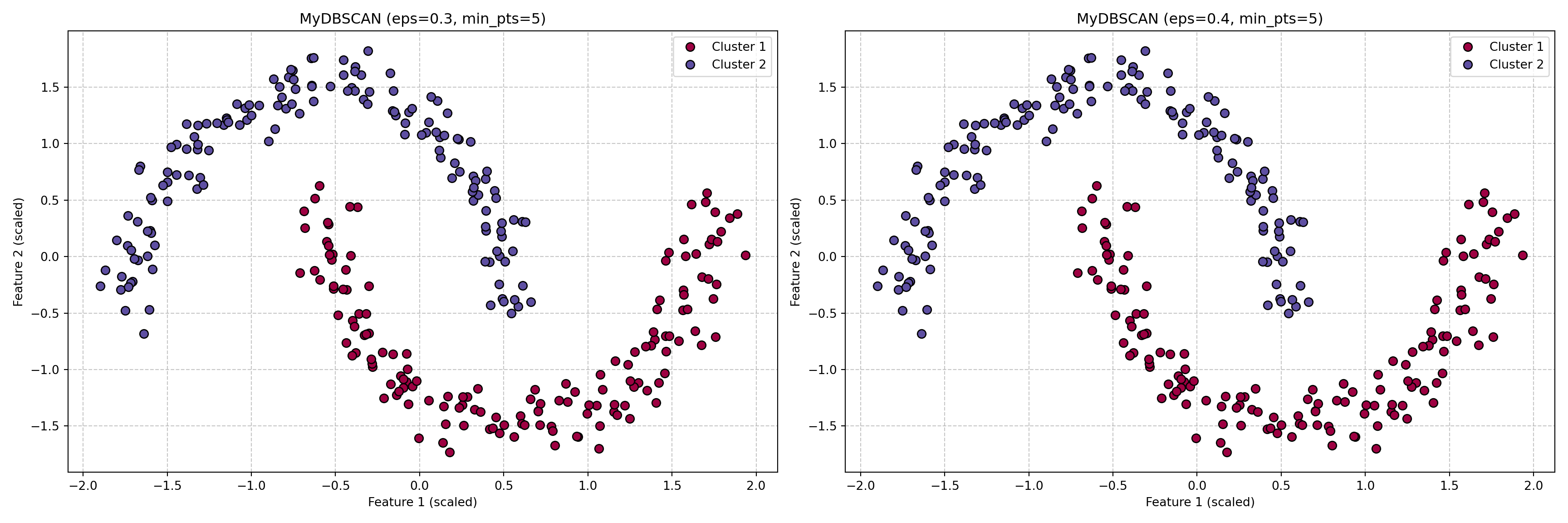

Code

print(f"\nAvec MyDBSCAN (eps={my_dbscan_custom_eps03_mp5.eps}, min_pts={my_dbscan_custom_eps03_mp5.min_pts}):")


Avec MyDBSCAN (eps=0.3, min_pts=5):

Code

print(f"Nombre de clusters trouvés (hors bruit): {my_dbscan_custom_eps03_mp5.n_clusters_}")

Nombre de clusters trouvés (hors bruit): 2

Code

print(f"Nombre de points de bruit: {np.sum(clusters_custom_03_5 == -1)}")

Nombre de points de bruit: 0

Code

print(f"\nAvec MyDBSCAN (eps={my_dbscan_custom_eps04_mp5.eps}, min_pts={my_dbscan_custom_eps04_mp5.min_pts}):")


Avec MyDBSCAN (eps=0.4, min_pts=5):

Code

print(f"Nombre de clusters trouvés (hors bruit): {my_dbscan_custom_eps04_mp5.n_clusters_}")

Nombre de clusters trouvés (hors bruit): 2

Code

print(f"Nombre de points de bruit: {np.sum(clusters_custom_04_5 == -1)}")

Nombre de points de bruit: 0

7.3 Application de l’implémentation de scikit-learn

Code

# Paramètres pour scikit-learn DBSCAN (les mêmes que testés précédemment)
dbscan_sklearn = DBSCAN(eps=0.3, min_samples=5)
clusters_sklearn_03_5 = dbscan_sklearn.fit_predict(X_moons_scaled)

dbscan_sklearn_04_5 = DBSCAN(eps=0.4, min_samples=5)
clusters_sklearn_04_5 = dbscan_sklearn_04_5.fit_predict(X_moons_scaled)


# --- Visualisation des résultats de scikit-learn DBSCAN ---
plt.figure(figsize=(18, 6))

# Graphique pour eps=0.3, min_samples=5
plt.subplot(1, 2, 1)
unique_labels_s_03_5 = np.unique(clusters_sklearn_03_5)
colors_s_03_5 = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels_s_03_5))]

for k, col in zip(unique_labels_s_03_5, colors_s_03_5):
    if k == -1: # Bruit
        col = [0, 0, 0, 1] # Noir

    class_member_mask = (clusters_sklearn_03_5 == k)
    xy = X_moons_scaled[class_member_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=7,
             label=f'Cluster {k}' if k != -1 else 'Bruit')

plt.title(f'Scikit-learn DBSCAN (eps=0.3, min_samples=5)')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)

# Graphique pour eps=0.4, min_samples=5
plt.subplot(1, 2, 2)
unique_labels_s_04_5 = np.unique(clusters_sklearn_04_5)
colors_s_04_5 = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels_s_04_5))]

for k, col in zip(unique_labels_s_04_5, colors_s_04_5):
    if k == -1: # Bruit
        col = [0, 0, 0, 1] # Noir

    class_member_mask = (clusters_sklearn_04_5 == k)
    xy = X_moons_scaled[class_member_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=7,
             label=f'Cluster {k}' if k != -1 else 'Bruit')

plt.title(f'Scikit-learn DBSCAN (eps=0.4, min_samples=5)')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()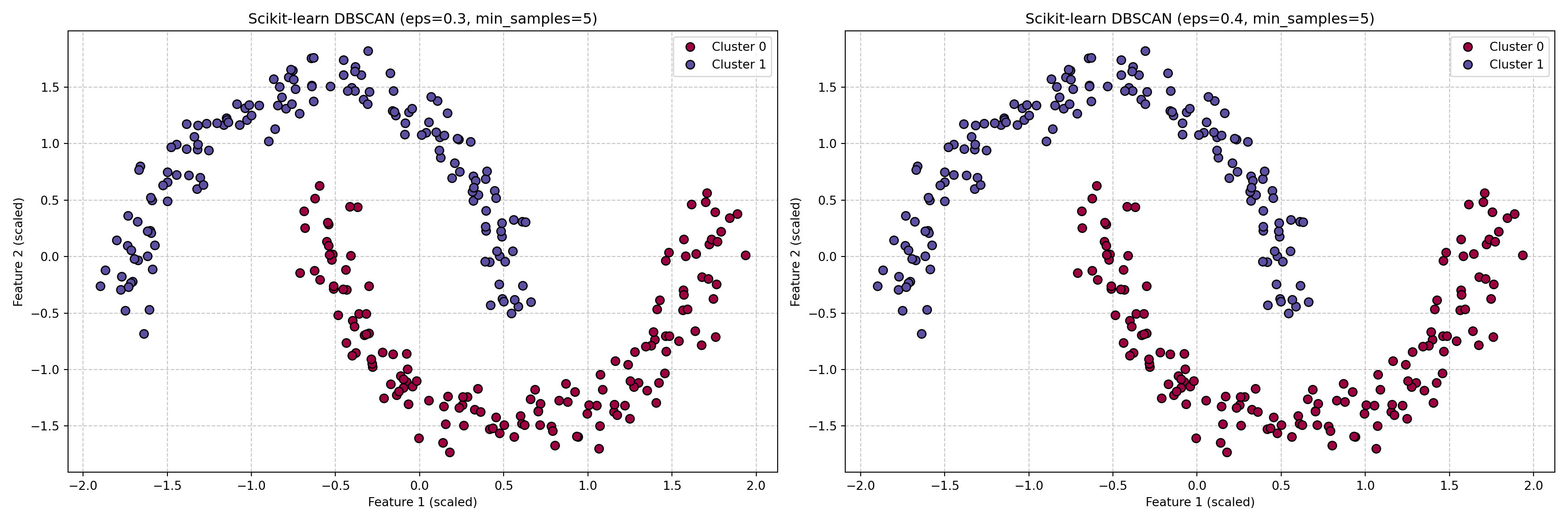

Code

num_clusters_sklearn_03_5 = len(np.unique(clusters_sklearn_03_5)) - (1 if -1 in clusters_sklearn_03_5 else 0)
num_noise_points_sklearn_03_5 = list(clusters_sklearn_03_5).count(-1)

num_clusters_sklearn_04_5 = len(np.unique(clusters_sklearn_04_5)) - (1 if -1 in clusters_sklearn_04_5 else 0)
num_noise_points_sklearn_04_5 = list(clusters_sklearn_04_5).count(-1)

print(f"\nAvec scikit-learn DBSCAN (eps=0.3, min_samples=5):")


Avec scikit-learn DBSCAN (eps=0.3, min_samples=5):

Code

print(f"Nombre de clusters trouvés (hors bruit): {num_clusters_sklearn_03_5}")

Nombre de clusters trouvés (hors bruit): 2

Code

print(f"Nombre de points de bruit: {num_noise_points_sklearn_03_5}")

Nombre de points de bruit: 0

Code

print(f"\nAvec scikit-learn DBSCAN (eps=0.4, min_samples=5):")


Avec scikit-learn DBSCAN (eps=0.4, min_samples=5):

Code

print(f"Nombre de clusters trouvés (hors bruit): {num_clusters_sklearn_04_5}")

Nombre de clusters trouvés (hors bruit): 2

Code

print(f"Nombre de points de bruit: {num_noise_points_sklearn_04_5}")

Nombre de points de bruit: 0

8 Exercice Pratique : Clustering de Documents d’Actualités avec SVD et DBSCAN

Objectif :

Dans cet exercice, vous allez appliquer DBSCAN pour découvrir des regroupements thématiques au sein d’un ensemble de documents d’actualités. Pour gérer la haute dimensionnalité des données textuelles, vous utiliserez d’abord la Décomposition en Valeurs Singulières (SVD) pour réduire la dimension.

Contexte :

L’analyse de grands volumes de textes non structurés, comme des articles de presse, est un défi courant. Le clustering peut aider à identifier automatiquement les sujets principaux abordés sans avoir besoin d’étiquettes prédéfinies. La SVD, souvent utilisée dans le cadre de l’Analyse Sémantique Latente (LSA), permet de projeter les données dans un espace de plus faible dimension tout en essayant de préserver la structure sémantique essentielle. L’analyse en composantes principales (ACP), dont la SVD est une méthode de calcul numériquement stable, vise à représenter les données de sorte à maximiser leur variance selon les nouvelles dimensions[cite: 1564, 1596]. Réduire la dimension est souvent nécessaire pour que les algorithmes basés sur des notions de similarité, comme DBSCAN, fonctionnent bien en grande dimension et pour contrer le “fléau de la dimension”[cite: 1519, 1520].

Données Suggérées :

Utilisez le jeu de données “20 Newsgroups”. Il est facilement accessible et contient des articles classés dans 20 catégories différentes, ce qui peut servir (avec précaution) de “vérité terrain” pour une évaluation qualitative ou externe a posteriori.

Étapes de l’Exercice :

Chargement et Prétraitement des Données :
- Chargez une partie du jeu de données “20 Newsgroups” (par exemple, sélectionnez 4 à 5 catégories pour simplifier l’analyse initiale ou utilisez l’ensemble complet).
- Effectuez un prétraitement standard du texte :
  - Nettoyage (suppression des en-têtes, pieds de page, citations des e-mails si présents, caractères spéciaux, etc.).
  - Tokenisation.
  - Conversion en minuscules.
  - Suppression des mots vides (stop words).
  - Racinisation (Stemming) ou Lemmatisation.
Vectorisation des Textes :
- Transformez les documents prétraités en une matrice numérique à l’aide de la méthode TF-IDF. Chaque ligne représentera un document et chaque colonne un terme du vocabulaire.
Réduction de Dimension avec SVD :
- Appliquez la SVD (ou TruncatedSVD de scikit-learn qui est adaptée aux matrices éparses comme TF-IDF) à la matrice TF-IDF.
- Choisissez un nombre de composantes à conserver (par exemple, 50, 100, ou utilisez un critère comme le pourcentage de variance expliquée si vous passez par une ACP via SVD sur une matrice dense, bien que ce soit moins direct avec TruncatedSVD sur TF-IDF). Le but de la réduction de dimension est de transformer une représentation $X \in \mathbb{R}^{n \times p}$ des données en une représentation $X^* \in \mathbb{R}^{n \times m}$ où $m \ll p$.
Application de DBSCAN :
- Sur les données de dimension réduite obtenues à l’étape précédente, appliquez votre implémentation MyDBSCAN ou la version de scikit-learn.
- Vous devrez choisir une métrique de distance appropriée (la distance Euclidienne est souvent utilisée sur les sorties de SVD/LSA, ou la distance cosinus si l’interprétation angulaire est préférée).
- Ajustez les paramètres eps et minPts de DBSCAN. Cela nécessitera probablement plusieurs essais :
  - Utilisez la méthode du k-distance plot pour vous aider à estimer eps.
  - Commencez avec une valeur de minPts (par exemple, 5-10) et ajustez-la.
Analyse et Évaluation des Clusters :
- Combien de clusters ont été trouvés par DBSCAN ?
- Combien de points ont été classés comme bruit ?
- Pour chaque cluster significatif :
  - Examinez les termes les plus fréquents ou ayant les scores TF-IDF les plus élevés parmi les documents du cluster (avant la SVD) pour essayer de nommer ou de caractériser le thème du cluster.
  - Lisez quelques documents de chaque cluster pour valider qualitativement sa cohérence.
- Si vous avez conservé les étiquettes originales des catégories du “20 Newsgroups”, vous pouvez (avec précaution, car le clustering est non supervisé) comparer les clusters trouvés aux catégories réelles en utilisant des métriques d’évaluation externe comme l’Indice de Rand Ajusté (ARI) ou l’Information Mutuelle Normalisée (NMI).

Questions pour la Réflexion :

Quel a été l’impact de la réduction de dimension par SVD sur la performance (temps de calcul, qualité subjective des clusters) de DBSCAN ?
Comment le choix de eps et minPts a-t-il influencé les résultats ? Décrivez votre processus d’ajustement.
Les clusters trouvés correspondent-ils intuitivement à des sujets distincts ? Y a-t-il des surprises ?
Les documents classés comme “bruit” par DBSCAN semblent-ils effectivement être des outliers ou des documents difficiles à classer ?

Bonus :

Comparez les résultats de DBSCAN avec ceux d’un autre algorithme de clustering (par exemple, K-Means) sur les mêmes données (réduites en dimension). Quelles sont les différences observées ?
Visualisez les clusters en 2D après une étape de réduction de dimension supplémentaire (par exemple, avec t-SNE) appliquée aux vecteurs issus de la SVD, en colorant les points selon les clusters DBSCAN.

Code

# Librairies
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer
import nltk
nltk.download('stopwords')

True

Code

nltk.download('wordnet2021')

True

Code

import re
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer, WordNetLemmatizer

Code

# Download NLTK resources if not already downloaded
try:
    nltk.data.find('corpora/stopwords')
except nltk.downloader.DownloadError:
    nltk.download('stopwords')

FileSystemPathPointer('/home/toussile/nltk_data/corpora/stopwords')

Code

# --- 1. Chargement et Prétraitement des Données ---

# Chargez une partie du jeu de données (par exemple, 4 catégories)
categories = ['alt.atheism', 'soc.religion.christian', 'comp.graphics', 'sci.med']
# categories = None # Uncomment to load all categories

print(f"Chargement des données des catégories: {categories if categories else 'Toutes'}")

Chargement des données des catégories: ['alt.atheism', 'soc.religion.christian', 'comp.graphics', 'sci.med']

Code

newsgroups_train = fetch_20newsgroups(subset='all',
                                      categories=categories,
                                      shuffle=True, random_state=42,
                                      remove=('headers', 'footers', 'quotes'))

documents = newsgroups_train.data
y_true_news = newsgroups_train.target # True labels (for potential evaluation)
target_names = newsgroups_train.target_names

print(f"Nombre de documents chargés: {len(documents)}")

Nombre de documents chargés: 3759

Code

# Prétraitement du texte
stop_words = set(stopwords.words('english'))
stemmer = PorterStemmer()
lemmatizer = WordNetLemmatizer()

def preprocess_text(text):
    # Remove non-alphanumeric characters
    text = re.sub(r'\W', ' ', text)
    # Convert to lowercase
    text = text.lower()
    # Remove single characters
    text = re.sub(r'\s+[a-zA-Z]\s+', ' ', text)
    # Remove multiple spaces
    text = re.sub(r'\s+', ' ', text, flags=re.I)
    # Tokenization
    tokens = text.split()
    # Remove stop words and stem or lemmatize
    processed_tokens = []
    for word in tokens:
        if word not in stop_words:
            # Use stemming or lemmatization - choose one
            # processed_tokens.append(stemmer.stem(word))
            processed_tokens.append(lemmatizer.lemmatize(word))
    return ' '.join(processed_tokens)

print("Prétraitement des documents...")

Prétraitement des documents...

Code

processed_documents = [preprocess_text(doc) for doc in documents]
print("Prétraitement terminé.")

Prétraitement terminé.

Code

# --- 2. Vectorisation des Textes (TF-IDF) ---

print("Vectorisation avec TF-IDF...")

Vectorisation avec TF-IDF...

Code

vectorizer = TfidfVectorizer(max_df=0.95, min_df=2,
                             max_features=10000) # Limit features
tfidf_matrix = vectorizer.fit_transform(processed_documents)
print(f"Dimensions de la matrice TF-IDF : {tfidf_matrix.shape}")

Dimensions de la matrice TF-IDF : (3759, 10000)

Code

# --- 3. Réduction de Dimension avec SVD ---

print("Réduction de dimension avec TruncatedSVD...")

Réduction de dimension avec TruncatedSVD...

Code

n_components = 100 # Nombre de composantes à conserver
svd = TruncatedSVD(n_components=n_components, random_state=42)

# Pipeline pour SVD et Normalisation (souvent utile pour les algorithmes basés sur la distance)
lsa = make_pipeline(svd, Normalizer(copy=False))

X_reduced = lsa.fit_transform(tfidf_matrix)
print(f"Dimensions des données après SVD : {X_reduced.shape}")

Dimensions des données après SVD : (3759, 100)

La réduction de dimensions à été faite. Il reste mainntenant à faire le clustering.

Copyright

2025 W. Toussile

1 Introduction au Clustering et à DBSCAN

1.1 Qu’est-ce que le clustering ?

1.2 Pourquoi DBSCAN ?

1.3 \(K\)-Means vs DBSCAN

2 Concepts fondamentaux

2.1 Définitions Clés

2.2 Structure d’un Cluster

3 L’Algorithme DBSCAN Étape par Étape ⚙️

3.1 Algorithme Détaillé

4 Choix des Paramètres `eps` et `minPts` pour DBSCAN ⚙️

4.1 Choix de `minPts`

4.2 Choix de `eps` (\(\epsilon\))

4.3 Interaction entre `eps` et `minPts`

4.4 Approche Itérative et Évaluation

4.5 Considérations pour des Densités Variables

4.6 La Métrique de Distance

5 Avantages et Inconvénients de DBSCAN ⚖️

5.1 Avantages de DBSCAN

5.2 Inconvénients de DBSCAN

6 Évaluation des Résultats de DBSCAN 📊

6.1 Évaluation Interne (sans vérité terrain)

Homogénéité (Compacité / Tightness)

Séparabilité

Indice de Davies-Bouldin

Coefficient de Silhouette

Stabilité des Clusters

6.2 Évaluation Externe (avec vérité terrain)

Indice de Rand

7 Implémentation Pratique de MyDBSCAN et Test 💻

7.1 Notre implémentation

7.2 Test sur données simulées

7.3 Application de l’implémentation de scikit-learn

8 Exercice Pratique : Clustering de Documents d’Actualités avec SVD et DBSCAN

Copyright

1 Introduction au Clustering et à DBSCAN

1.1 Qu’est-ce que le clustering ?

1.2 Pourquoi DBSCAN ?

1.3 \(K\)-Means vs DBSCAN

2 Concepts fondamentaux

2.1 Définitions Clés

2.2 Structure d’un Cluster

3 L’Algorithme DBSCAN Étape par Étape ⚙️

3.1 Algorithme Détaillé

4 Choix des Paramètres eps et minPts pour DBSCAN ⚙️

4.1 Choix de minPts

4.2 Choix de eps (\(\epsilon\))

4.3 Interaction entre eps et minPts

4.4 Approche Itérative et Évaluation

4.5 Considérations pour des Densités Variables

4.6 La Métrique de Distance

5 Avantages et Inconvénients de DBSCAN ⚖️

5.1 Avantages de DBSCAN

5.2 Inconvénients de DBSCAN

6 Évaluation des Résultats de DBSCAN 📊

6.1 Évaluation Interne (sans vérité terrain)

Homogénéité (Compacité / Tightness)

Séparabilité

Indice de Davies-Bouldin

Coefficient de Silhouette

Stabilité des Clusters

6.2 Évaluation Externe (avec vérité terrain)

Indice de Rand

7 Implémentation Pratique de MyDBSCAN et Test 💻

7.1 Notre implémentation

7.2 Test sur données simulées

7.3 Application de l’implémentation de scikit-learn

8 Exercice Pratique : Clustering de Documents d’Actualités avec SVD et DBSCAN

Copyright

4 Choix des Paramètres `eps` et `minPts` pour DBSCAN ⚙️

4.1 Choix de `minPts`

4.2 Choix de `eps` (\(\epsilon\))

4.3 Interaction entre `eps` et `minPts`