Avant et Après : Mesurer un Changement avec le t-test pour Échantillons Appariés

1 Quand les Groupes sont Liés

Dans les articles précédents, nous avons appris à comparer des groupes indépendants. Mais que se passe-t-il lorsque nos mesures sont intrinsèquement liées ?

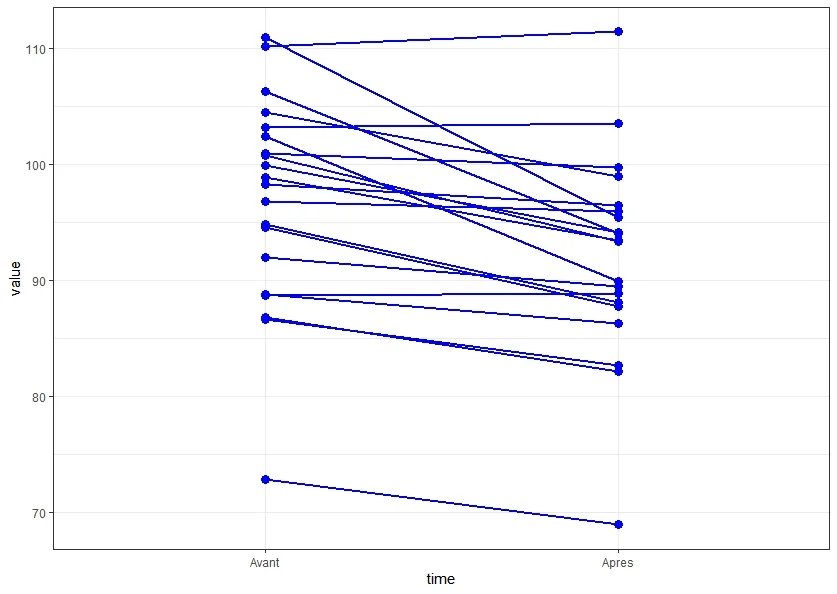
Imaginez que vous voulez mesurer l’efficacité d’un programme de formation. Le moyen le plus fiable n’est pas de comparer un groupe formé à un autre groupe non formé, mais de mesurer les compétences des mêmes employés avant, puis après la formation. Les deux mesures pour chaque employé sont “appariées” ou “dépendantes”.

Pour analyser ce type de données, nous avons besoin d’un outil spécifique : le t-test pour échantillons appariés (ou pairés).

2 Le Scénario Clé : Quand l’utiliser ?

Ce test est votre meilleur allié lorsque vos observations se présentent par paires. Chaque observation dans le premier échantillon est directement associée à une et une seule observation dans le second.

Cas d’usage typiques :

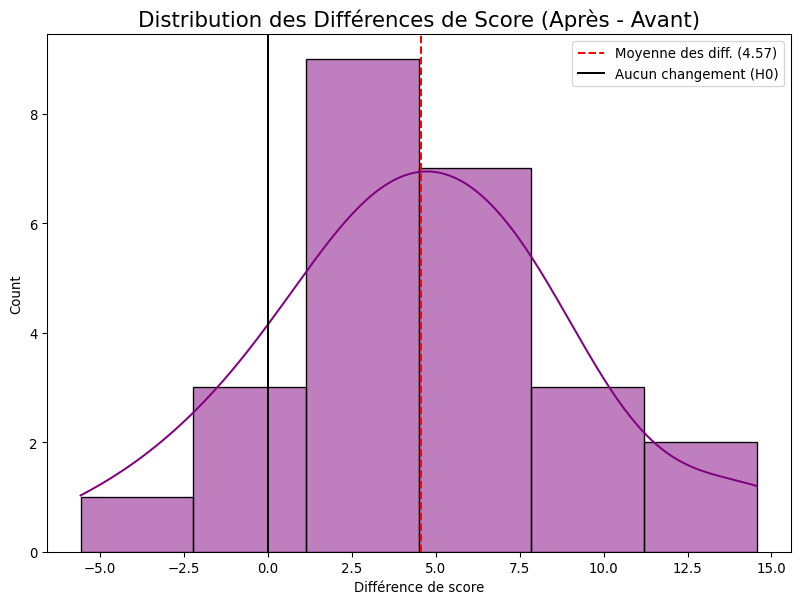
Études “Avant-Après” : Mesurer un indicateur (poids, score, tension artérielle) sur les mêmes sujets avant et après une intervention.
Comparaison de deux méthodes : Les mêmes sujets utilisent deux outils différents (ex: deux claviers d’ordinateur) et on mesure leur performance sur chacun.
Paires naturelles : Études sur des jumeaux, où chaque jumeau d’une paire est assigné à un groupe différent.

3 L’Astuce Géniale : Un Test à un Échantillon Déguisé

La beauté du t-test pour échantillons appariés est qu’il n’est pas un nouveau test complexe. C’est en réalité une application très intelligente du t-test à un échantillon que nous connaissons déjà !

Voici la logique, en trois étapes simples :

Calculer les Différences : Pour chaque paire, on calcule la différence entre la deuxième et la première mesure (ex: score_après - score_avant).
Créer un Nouvel Échantillon : On obtient alors une nouvelle et unique colonne de données : la liste de toutes ces différences.
Tester la Moyenne des Différences : On réalise un t-test à un échantillon sur cette nouvelle colonne de différences.

L’hypothèse nulle devient alors :

\(H_0\) (Hypothèse Nulle) : La moyenne des différences dans la population est égale à zéro. \[ H_0: \mu_{\text{différence}} = 0 \]

En d’autres termes, on teste si, en moyenne, il n’y a eu aucun changement entre la première et la seconde mesure.

4 Atelier Pratique : L’Efficacité d’une Formation

L’entreprise Innovatech a mis en place une formation pour améliorer les compétences de ses chefs de projet. Pour en mesurer l’efficacité, elle a évalué les compétences de 25 d’entre eux sur 100 points, avant et après la formation.

Les données sont-elles suffisantes pour prouver que la formation a eu un effet positif ?

import pandas as pd
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt

# --- 1. Création des données ---
np.random.seed(123)
n = 25
# Scores avant la formation
score_avant = np.random.normal(loc=65, scale=8, size=n).clip(40, 90)
# Scores après : on ajoute un effet positif moyen de 5 points + du bruit
effet_formation = np.random.normal(loc=5, scale=4, size=n)
score_apres = (score_avant + effet_formation).clip(40, 100)

df = pd.DataFrame({'score_avant': score_avant, 'score_apres': score_apres})

# --- 2. Calcul des différences ---
df['difference'] = df['score_apres'] - df['score_avant']

print("--- Étape 2: Aperçu des données et des différences ---")
print(df.head())
print(f"\nMoyenne des différences: {df['difference'].mean():.2f}\n")

# --- 3. Visualisation des différences ---
# Il est très utile de visualiser la distribution des différences.
# C'est sur cette distribution que le test est effectué.
plt.figure(figsize=(10, 7))
sns.histplot(df['difference'], kde=True, color='purple')
plt.axvline(df['difference'].mean(), color='red', linestyle='--', label=f"Moyenne des diff. ({df['difference'].mean():.2f})")
plt.axvline(0, color='black', linestyle='-', label="Aucun changement (H0)")
plt.title("Distribution des Différences de Score (Après - Avant)", fontsize=16)
plt.xlabel("Différence de score")
plt.legend()
plt.show()

# --- 4. Poser les hypothèses ---
# H0: La moyenne des différences est de 0 (la formation n'a pas d'effet).
# H1: La moyenne des différences est différente de 0.

# --- 5. Réalisation du test ---
# On utilise ttest_rel de scipy.stats, qui est faite pour les échantillons appariés.
# Elle calcule les différences et fait le test en une seule étape.
t_statistic, p_value = stats.ttest_rel(a=df['score_apres'], b=df['score_avant'])

print("\n--- Étape 5: Résultat du t-test pour Échantillons Appariés ---")
print(f"Statistique t calculée: {t_statistic:.3f}")
print(f"P-value (bilatérale): {p_value:.8f}\n") # Afficher plus de décimales pour les p-values très faibles

# --- 6. Interprétation et Conclusion ---
alpha = 0.05

print("--- Étape 6: Conclusion ---")
if p_value < alpha:
    print(f"Décision: Rejeter H0 (car {p_value:.8f} < {alpha}).")
    print("Conclusion: Nous avons une preuve statistiquement très solide que la formation a eu un effet significatif sur les scores de compétence.")
else:
    print(f"Décision: Ne pas rejeter H0 (car {p_value:.8f} >= {alpha}).")
    print("Conclusion: Nous n'avons pas de preuve suffisante pour conclure à un effet de la formation.")

--- Étape 2: Aperçu des données et des différences ---
   score_avant  score_apres  difference
0    56.314955    58.763949    2.448994
1    72.978764    81.607184    8.628421
2    67.263828    66.549105   -0.714723
3    52.949642    57.389367    4.439725
4    60.371198    61.924178    1.552980

Moyenne des différences: 4.57


--- Étape 5: Résultat du t-test pour Échantillons Appariés ---
Statistique t calculée: 4.890
P-value (bilatérale): 0.00005493

--- Étape 6: Conclusion ---
Décision: Rejeter H0 (car 0.00005493 < 0.05).
Conclusion: Nous avons une preuve statistiquement très solide que la formation a eu un effet significatif sur les scores de compétence.

Analyse du Résultat

La p-value obtenue est extrêmement faible (beaucoup plus petite que notre seuil de 0.05). La visualisation confirme que la grande majorité des différences sont positives, et que leur moyenne est bien loin de zéro.
Conclusion en français simple : La probabilité d’observer une telle amélioration moyenne des scores si la formation n’avait eu aucun effet est infime. Nous pouvons donc rejeter l’hypothèse nulle avec une grande confiance et conclure que le programme de formation a été efficace pour augmenter les compétences des chefs de projet.

5 Conclusion

Le t-test pour échantillons appariés est un outil élégant et puissant. En transformant un problème à deux échantillons en un problème à un seul échantillon de différences, il nous permet d’isoler et de mesurer l’effet d’une intervention de manière très précise.

Et maintenant ?

Nous avons maintenant une boîte à outils complète pour comparer une ou deux moyennes. Mais que se passe-t-il lorsque la réalité est plus complexe ? Comment comparer les scores de satisfaction dans 3, 4, ou même 10 départements différents à la fois ? Tenter de faire des t-tests entre chaque paire serait une grave erreur! Dans notre prochain et dernier article de cette série, nous découvrirons la solution : l’Analyse de la Variance (ANOVA).