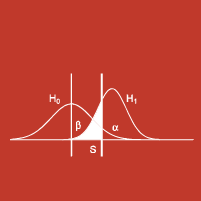
1 Pourquoi faire des tests ?
En tant qu’analystes de données, nous sommes des détectives. Notre mission ? Utiliser les données pour confirmer ou infirmer des théories. Mais comment être sûr que ce que nous observons n’est pas simplement dû au hasard ?
C’est là qu’interviennent les tests statistiques. Ils nous fournissent un cadre rigoureux pour prendre des décisions basées sur des preuves (nos données), et non sur de simples intuitions.
Ce post vous explique les 4 principes fondamentaux qui se cachent derrière tous les tests statistiques, du plus simple au plus complexe.
2 Principe 1 : Le Procès des Hypothèses
Imaginez un procès au tribunal. Il y a toujours deux versions de l’histoire qui s’affrontent :
- L’accusé est présumé innocent : C’est la situation par défaut, le statu quo.
- L’accusé est coupable : C’est la nouvelle théorie que le procureur essaie de prouver.
En statistique, c’est exactement la même chose. Nous avons deux hypothèses concurrentes :
L’Hypothèse Nulle (\(H_0\)) : C’est la “présomption d’innocence”. Elle affirme qu’il n’y a pas d’effet, pas de différence, pas de relation. C’est le statu quo.
- Exemple : “Le nouveau médicament n’a aucun effet sur la tension artérielle.”
L’Hypothèse Alternative (\(H_1\) ou \(H_a\)) : C’est la théorie du “procureur”. Elle affirme qu’il y a un effet, une différence, une relation. C’est ce que nous cherchons à prouver.
- Exemple : “Le nouveau médicament fait baisser la tension artérielle.”
Le but d’un test statistique n’est jamais de prouver que l’hypothèse alternative est vraie. Son but est de déterminer si nous avons suffisamment de preuves pour rejeter l’hypothèse nulle.
3 Principe 2 : La Preuve (La Statistique de Test)
Au tribunal, le procureur présente des preuves (empreintes, témoignages…). En statistique, nous collectons des données et nous les résumons en un seul chiffre : la statistique de test.
Ce chiffre (un score Z, un t de Student, un Chi-carré, etc.) mesure l’écart entre ce que nous avons observé dans nos données et ce que nous nous attendrions à voir si l’hypothèse nulle (\(H_0\)) était vraie.
Plus la statistique de test est “extrême” (grande ou petite), plus nos données sont “bizarres” ou “inattendues” sous l’hypothèse du statu quo (\(H_0\)).
4 Principe 3 : Le Verdict (La p-value)
C’est le concept le plus important, mais souvent le plus mal compris.
La p-value (ou valeur-p) est une probabilité. Elle répond à la question suivante :
“Si l’hypothèse nulle (\(H_0\)) était réellement vraie, quelle serait la probabilité d’observer des données au moins aussi extrêmes que celles que nous avons collectées ?”
Revenons à notre procès :
- Une p-value élevée (ex: 0.80) signifie : “Si l’accusé était innocent, il y aurait 80% de chances de trouver des preuves comme celles-ci. Ce n’est donc pas surprenant.” -> On ne peut pas rejeter l’innocence.
- Une p-value faible (ex: 0.01) signifie : “Si l’accusé était innocent, il n’y aurait que 1% de chances de trouver des preuves aussi accablantes. C’est extrêmement surprenant !” -> On a de fortes raisons de rejeter l’innocence.
Une p-value faible ne mesure pas la probabilité que \(H_0\) soit vraie. Elle mesure la compatibilité de nos données avec \(H_0\). Une faible compatibilité nous pousse à rejeter \(H_0\).
5 Principe 4 : La Sentence (La Décision)
Comment décider si une p-value est “suffisamment faible” ? Nous fixons une règle avant de commencer le test. C’est le seuil de significativité, noté alpha (\(\alpha\)).
La valeur la plus courante pour \(\alpha\) est 0.05 (soit 5%). C’est notre “seuil de doute raisonnable”.
La règle de décision est simple :
Si p-value < \(\alpha\) (ex: 0.01 < 0.05) : Le résultat est statistiquement significatif. Nous avons suffisamment de preuves pour rejeter l’hypothèse nulle (\(H_0\)) en faveur de l’hypothèse alternative (\(H_1\)).
- Conclusion : “Nous rejetons l’idée que le médicament n’a pas d’effet.”
Si p-value ≥ \(\alpha\) (ex: 0.34 > 0.05) : Le résultat est non statistiquement significatif. Nous n’avons pas suffisamment de preuves pour rejeter l’hypothèse nulle (\(H_0\)).
- Conclusion : “Nous ne pouvons pas rejeter l’idée que le médicament n’a pas d’effet.” (Attention, cela ne prouve pas que \(H_0\) est vraie !)
6 Résumé du Processus
| Étape du Procès | Étape Statistique | Description |
|---|---|---|
| Présomption | 1. Formuler les Hypothèses (\(H_0, H_1\)) | Définir le statu quo et la théorie à tester. |
| Présentation des preuves | 2. Calculer la Statistique de Test | Résumer l’écart entre les données observées et les attentes sous \(H_0\). |
| Délibération du jury | 3. Calculer la p-value | Évaluer la probabilité d’obtenir ces preuves si \(H_0\) était vraie. |
| Verdict final | 4. Prendre une Décision (avec \(\alpha\)) | Comparer la p-value au seuil de significativité pour rejeter ou non \(H_0\). |
En maîtrisant ces quatre principes, vous comprenez la logique qui anime l’ensemble des statistiques inférentielles. Vous êtes prêt à mener vos propres enquêtes avec rigueur et confiance !