1 Introduction : Les Arbitres de nos Données
Dans nos articles précédents, nous avons vu qu’un test statistique se résume à calculer une statistique de test. Ce chiffre mesure à quel point nos données sont “surprenantes” par rapport à notre hypothèse nulle (\(H_0\)).
Mais comment décider si ce chiffre est vraiment surprenant ? Il nous faut un arbitre, un juge de paix. En statistique, cet arbitre est une loi de probabilité.
Chaque type de test statistique est associé à une loi de probabilité spécifique qui décrit le comportement de sa statistique de test si l’hypothèse nulle était vraie. C’est cette loi qui nous permet de calculer la fameuse p-value.
Ce post vous présente les quatre “grands juges” de la statistique inférentielle : les lois Normale, de Student, du Chi-carré et de Fisher.
2 L’Arsenal des Lois de Probabilité
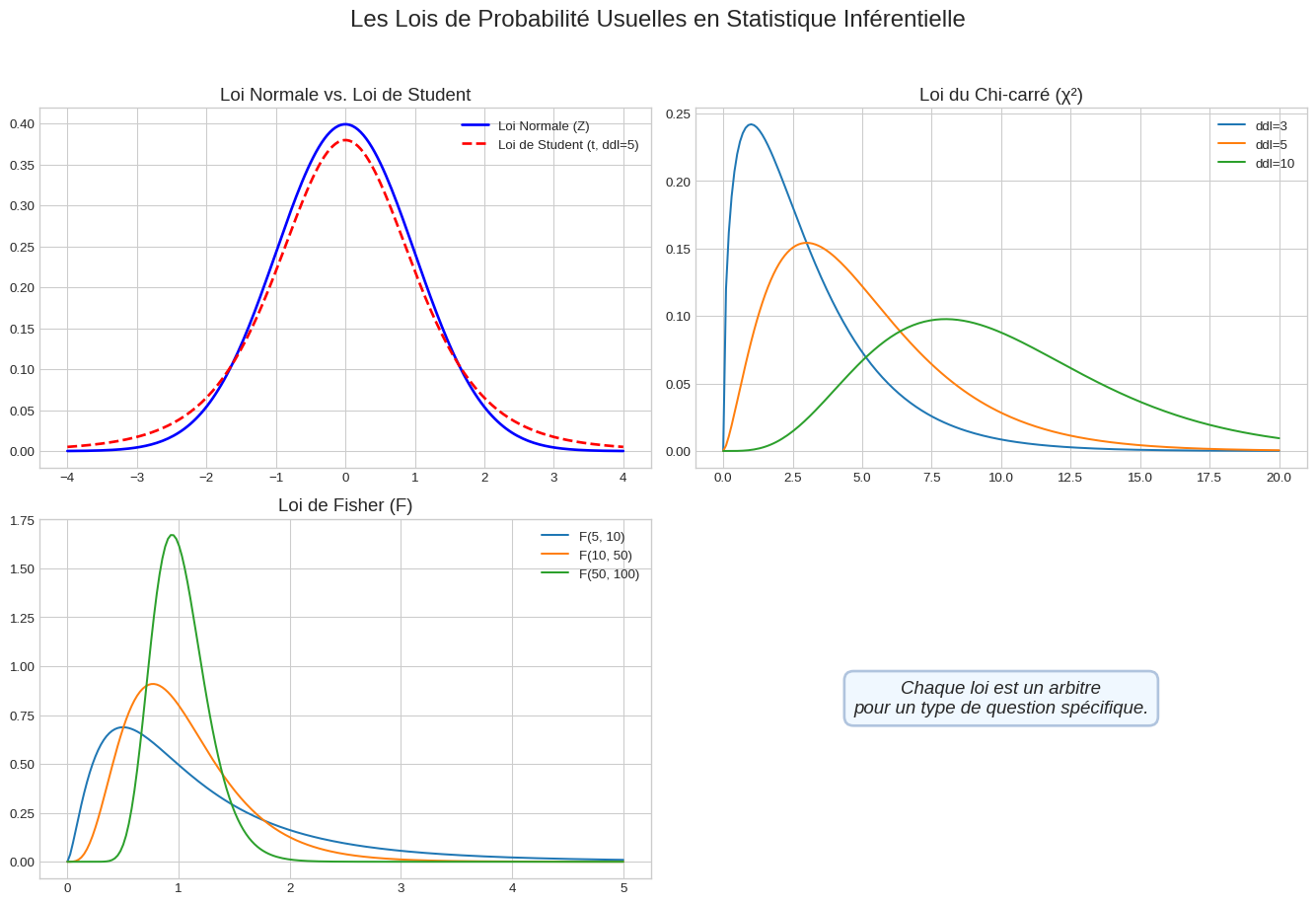
Visualisons ces quatre distributions clés. Chacune a une forme et des propriétés uniques, adaptées à des types de questions spécifiques.
2.1 1. La Loi Normale (Loi de Gauss)
- Le Contexte : C’est la reine des distributions. En théorie, on l’utilise pour le Z-test lorsque la variance de la population (\(\sigma^2\)) est connue, ce qui est rare en pratique. Elle est aussi la distribution limite pour les moyennes et les proportions sur de grands échantillons (merci le Théorème Central Limite !).
- La Statistique : Le Z-score, qui mesure l’écart à la moyenne en nombre d’écarts-types.
2.2 2. La Loi de Student (t)
- Le Contexte : C’est la distribution du praticien. On l’utilise pour le t-test lorsque la variance de la population est inconnue et doit être estimée à partir de l’échantillon.
- La Statistique : Le t-score.
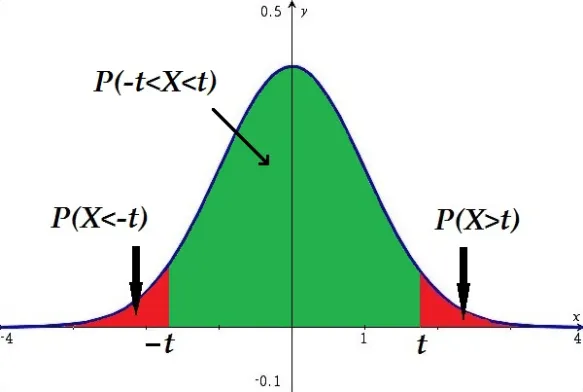
- La Différence Clé : Comme on le voit sur le graphique, la loi de Student a des “queues plus épaisses” que la loi Normale. Cela signifie qu’elle considère les valeurs extrêmes comme un peu plus probables, ce qui est une manière de prendre en compte l’incertitude supplémentaire liée à l’estimation de la variance. Elle dépend des degrés de liberté (ddl), liés à la taille de l’échantillon. Plus les ddl sont élevés, plus elle ressemble à la loi Normale.
2.3 3. La Loi du Chi-carré (\(\chi^2\))
- Le Contexte : C’est l’arbitre des données catégorielles. On l’utilise pour :
- Le test du \(\chi^2\) d’indépendance (y a-t-il un lien entre deux variables qualitatives ?).
- Le test du \(\chi^2\) d’ajustement (une distribution observée correspond-elle à une distribution théorique ?).
- La Statistique : La statistique du \(\chi^2\), qui additionne les écarts au carré entre les effectifs observés et les effectifs attendus.
- La Forme : Elle n’est définie que pour les valeurs positives et est asymétrique. Sa forme dépend de ses degrés de liberté.
2.4 4. La Loi de Fisher (F)
- Le Contexte : C’est la distribution qui permet de comparer des variances. Son application la plus célèbre est l’Analyse de la Variance (ANOVA), où l’on compare la variance entre les groupes à la variance à l’intérieur des groupes.
- La Statistique : Le F-score, qui est un ratio de deux variances.
- La Forme : Comme le Chi-carré, elle est positive et asymétrique. Sa forme est définie par deux degrés de liberté différents : un pour le numérateur et un pour le dénominateur.
3 Lois d’un Échantillon Gaussien
Maintenant que nous connaissons nos “juges”, voyons comment les statistiques calculées à partir de nos données se comportent. Le cadre de base est de supposer que nous avons un échantillon \((X_1, \dots, X_n)\) de variables indépendantes et identiquement distribuées (i.i.d.) issues d’une loi Normale de population \(N(\mu, \sigma^2)\).
Soit \(\bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i\) la moyenne empirique et \(S_n^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X}_n)^2\) la variance empirique (non biaisée).
Les résultats suivants sont les piliers de l’inférence statistique :
Distribution de la moyenne (si \(\sigma\) est connu) La statistique Z, qui standardise la moyenne de l’échantillon, suit une loi Normale standard. C’est la base du Z-test. \[Z = \frac{\sqrt{n}(\bar{X}_n - \mu)}{\sigma} \sim \mathcal{N}(0, 1)\]
Distribution de la variance La variance de l’échantillon, une fois normalisée, suit une loi du Chi-carré. C’est la base des tests de conformité d’une variance. \[\frac{(n-1)S_n^2}{\sigma^2} \sim \chi^2_{n-1}\]
Distribution de la moyenne (si \(\sigma\) est inconnu) C’est le cas le plus courant. En remplaçant \(\sigma\) par son estimation \(S_n\), la statistique T suit une loi de Student. C’est la base du t-test. \[T = \frac{\sqrt{n}(\bar{X}_n - \mu)}{S_n} \sim t_{n-1}\]
Distribution du ratio de deux variances Si l’on compare les variances de deux échantillons gaussiens indépendants, leur ratio suit une loi de Fisher. C’est la base du test F de Fisher pour l’égalité des variances et de l’ANOVA. \[F = \frac{S_{n_1}^2 / \sigma_1^2}{S_{n_2}^2 / \sigma_2^2} \sim F_{n_1-1, n_2-1}\]
4 Conclusion : Choisir le Bon Juge
Comprendre ces quatre distributions, c’est comprendre la mécanique interne des tests statistiques les plus courants. Le choix d’un test n’est rien d’autre que le choix de l’arbitre approprié pour juger de la force de vos preuves.
| Question posée | Test Commun | Statistique | Distribution (Juge) |
|---|---|---|---|
| Comparer une moyenne à une norme (\(\sigma\) inconnu) | t-test à 1 échantillon | t-score | Loi de Student |
| Comparer deux moyennes (\(\sigma\) inconnu) | t-test à 2 échantillons | t-score | Loi de Student |
| Y a-t-il un lien entre 2 variables qualitatives ? | Test du Chi-carré | \(\chi^2\)-score | Loi du Chi-carré |
| Comparer plus de 2 moyennes | ANOVA | F-score | Loi de Fisher |
En gardant ce tableau en tête, vous serez toujours en mesure de sélectionner l’outil statistique adéquat pour répondre à vos questions de recherche avec rigueur.