Introduction au Clustering : Trouver les Groupes dans vos Données

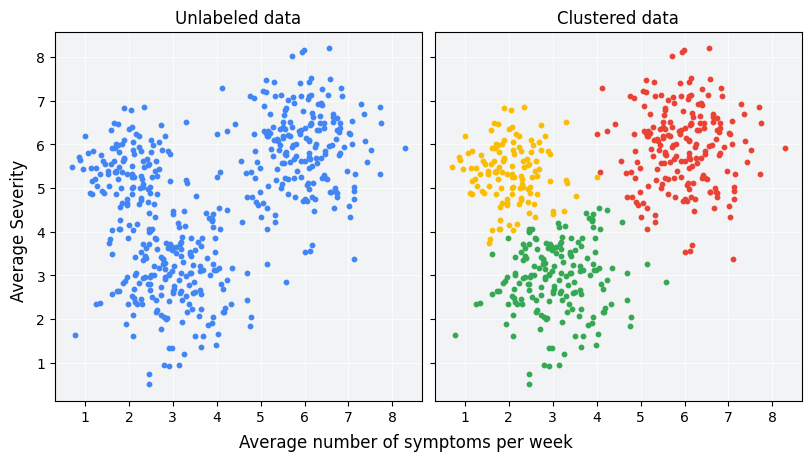
1 Introduction : Apprendre sans Étiquettes

Dans nos séries précédentes sur l’apprentissage supervisé, notre mission était toujours guidée par une cible, une “bonne réponse” (\(y_i\)) que nous cherchions à prédire. Nous entrons maintenant dans un nouveau territoire fascinant : l’apprentissage non supervisé.

Ici, il n’y a pas de professeur, pas d’étiquettes. Nous disposons d’un ensemble de données et nous posons à l’algorithme une question beaucoup plus ouverte : “Y a-t-il une structure cachée ici ? Peux-tu trouver des groupes naturels dans ces données ?”

Le clustering est la tâche la plus fondamentale de l’apprentissage non supervisé. C’est l’art et la science de regrouper des objets de telle sorte que ceux qui se trouvent dans le même groupe (ou cluster) soient plus similaires les uns aux autres que ceux qui se trouvent dans d’autres groupes.

Ce post va poser les bases conceptuelles et pratiques du clustering, qui nous serviront tout au long de cette nouvelle série.

2 Le Problème du Clustering : Formalisation

De manière formelle, étant donné un jeu de données non étiqueté \(D_n = \{x_i\}_{i=1}^n\), où chaque \(x_i\) est un vecteur de caractéristiques dans un espace \(\mathcal{X}\), le but du clustering est de partitionner cet ensemble en \(K\) sous-ensembles (les clusters) \(C_1, C_2, \dots, C_K\).

Cette partition doit respecter deux principes :

• Haute cohésion intra-cluster : Les points au sein d’un même cluster \(C_k\) doivent être très similaires les uns aux autres.
• Faible couplage inter-cluster : Les points de clusters différents \(C_k\) et \(C_j\) (avec \(k \neq j\)) doivent être très différents les uns des autres.

3 Le Cœur du Problème : Similarité et Dissimilarité

Comment une machine peut-elle comprendre la notion de “ressemblance” ? Elle la traduit par un concept mathématique : la dissimilarité, qui est généralement mesurée par une distance.

L’idée est simple :

• Deux objets sont similaires si la distance entre eux est faible.
• Deux objets sont dissimilaires si la distance entre eux est élevée.

3.1 La Distance Euclidienne

Pour des données numériques, la mesure de distance la plus courante est la distance euclidienne. Pour deux points \(a = (a_1, \dots, a_p)\) et \(b = (b_1, \dots, b_p)\) dans un espace à \(p\) dimensions, elle est définie par : \[d(a, b) = \sqrt{\sum_{j=1}^{p} (a_j - b_j)^2}\] C’est simplement la longueur de la ligne droite qui relie les deux points. La quasi-totalité des algorithmes de clustering que nous verrons s’appuient sur cette mesure ou une de ses variantes.

4 Le Prérequis Indispensable : La Mise à l’Échelle des Variables

Puisque tout est basé sur les distances, nous faisons face à un problème majeur si nos variables n’ont pas la même échelle.

Imaginez que vous vouliez regrouper des personnes en fonction de deux variables :

• age (allant de 20 à 70 ans)
• salaire_annuel (allant de 30 000 à 150 000 €)

Dans le calcul de la distance euclidienne, la différence de salaire (un nombre très grand) va complètement écraser et rendre insignifiante la différence d’âge (un nombre très petit). Le clustering sera donc presque entièrement basé sur le salaire, ignorant l’information contenue dans l’âge.

Règle d’Or du Clustering

Avant d’appliquer un algorithme de clustering basé sur la distance, il est impératif de mettre toutes les variables à la même échelle. La méthode standard pour cela est la standardisation.

La standardisation (implémentée par StandardScaler dans Scikit-learn) transforme chaque variable pour qu’elle ait une moyenne de 0 et un écart-type de 1. Ainsi, toutes les variables ont un “poids” comparable dans le calcul de la distance.

5 La Feuille de Route : Les Grandes Familles de Clustering

Il n’existe pas un seul “meilleur” algorithme de clustering. Le choix dépend de la structure de vos données et de votre objectif. Nous explorerons trois grandes familles dans cette série :

1. Le Clustering par Partitionnement (Centroid-based) :

   • Idée : Diviser les données en \(K\) groupes non-chevauchants, où chaque groupe est représenté par un “centre” ou centroïde.
   • Champion : L’algorithme K-Means.
   • Idéal pour : Trouver des clusters de forme sphérique et de taille similaire.

2. Le Clustering Hiérarchique :

   • Idée : Créer une hiérarchie de clusters, soit en regroupant les points (approche agglomérative), soit en les divisant (approche divisive). Le résultat est un bel arbre appelé dendrogramme.
   • Avantage : Ne nécessite pas de choisir le nombre de clusters à l’avance.

3. Le Clustering Basé sur la Densité :

   • Idée : Regrouper les régions denses de l’espace, en les séparant des régions de faible densité.
   • Champion : L’algorithme DBSCAN.
   • Idéal pour : Découvrir des clusters de formes arbitraires (non sphériques) et identifier les points isolés comme du bruit (outliers).

6 Conclusion

Nous avons posé les bases de notre exploration du clustering. Nous avons défini le problème, compris le rôle central de la dissimilarité (mesurée par la distance) et identifié l’étape cruciale de la mise à l’échelle des données. Nous avons également un aperçu des différentes philosophies de clustering que nous allons découvrir.

Et maintenant ?

Il est temps de mettre les mains dans le cambouis ! Dans notre prochain article, nous plongerons en détail dans l’algorithme de clustering le plus célèbre et le plus utilisé : K-Means. Nous verrons comment il fonctionne et, surtout, comment répondre à sa question la plus difficile : “Comment choisir le bon nombre de clusters K ?”.

7 Exercices

Exercise 1  

Question 1

Quel est l’objectif principal du clustering en apprentissage non supervisé ?

1. Prédire une valeur numérique continue pour de nouvelles données.
2. Assigner des données à des catégories prédéfinies et étiquetées.
3. Découvrir des groupes naturels (clusters) dans des données non étiquetées.
4. Sélectionner les variables les plus importantes d’un jeu de données.

Question 2

Quelle est la “Règle d’Or” mentionnée dans l’article avant d’appliquer un algorithme de clustering ?

1. Toujours supprimer les valeurs aberrantes (outliers).
2. S’assurer que le jeu de données contient plus de 1000 observations.
3. Mettre toutes les variables à la même échelle (par exemple, par standardisation).
4. Choisir le nombre de clusters K avant toute autre étape.

Question 3

Pourquoi la mise à l’échelle des variables est-elle si importante pour le clustering ?

1. Pour que l’algorithme s’exécute plus rapidement.
2. Pour éviter que les variables avec de grandes échelles de valeurs n’écrasent l’influence des variables avec de petites échelles.
3. C’est une convention qui n’a pas d’impact réel sur le résultat.
4. Pour transformer les données non-numériques en données numériques.

Question 4

Comment la plupart des algorithmes de clustering mesurent-ils la “similarité” entre deux points ?

1. En calculant leur corrélation.
2. En calculant une distance (comme la distance euclidienne) entre eux.
3. En comptant le nombre de variables où ils ont la même valeur.
4. En utilisant un test statistique.

Question 5

L’algorithme K-Means est le champion de quelle famille de clustering ?

1. Le clustering hiérarchique.
2. Le clustering basé sur la densité.
3. Le clustering par partitionnement (basé sur les centroïdes).
4. Le clustering supervisé.

Question 6

Quel est le principal avantage du clustering hiérarchique mentionné dans l’introduction ?

1. Il est idéal pour trouver des clusters de formes non-sphériques.
2. Il ne nécessite pas de choisir le nombre de clusters à l’avance.
3. C’est l’algorithme de clustering le plus rapide.
4. Il est très robuste au bruit et aux outliers.

Question 7

Pour quel type de problème l’algorithme DBSCAN est-il particulièrement bien adapté ?

1. Pour des jeux de données très petits.
2. Pour trouver des clusters de formes arbitraires et identifier le bruit.
3. Quand tous les clusters sont sphériques et de même taille.
4. Quand les données sont parfaitement séparées sans aucun chevauchement.

Question 8

Que signifie le principe de “haute cohésion intra-cluster” ?

1. Les clusters sont très différents les uns des autres.
2. Chaque cluster contient le même nombre de points.
3. Les points à l’intérieur d’un même cluster sont très similaires entre eux.
4. Les clusters forment une hiérarchie claire.

Question 9

La standardisation, implémentée par StandardScaler dans Scikit-learn, transforme chaque variable pour qu’elle ait…

1. …une valeur minimale de 0 et une valeur maximale de 1.
2. …une moyenne de 0 et un écart-type de 1.
3. …uniquement des valeurs entières.
4. …une distribution normale.

Question 10

Le clustering est une tâche d’apprentissage…

1. …supervisé, car on cherche à prédire une cible.
2. …non supervisé, car on travaille avec des données non étiquetées.
3. …par renforcement, car l’algorithme apprend par essais et erreurs.
4. …semi-supervisé, car on a quelques étiquettes.