1 Qu’est-ce que la Régression ?
Dans notre exploration du Machine Learning, nous avons vu que les algorithmes peuvent être classés en plusieurs familles. L’une des plus importantes et des plus utiles est la régression.
Le problème de la régression se pose chaque fois que nous cherchons à répondre à une question de type “Combien ?” ou “À quel point ?”.
En termes simples, la régression est une technique statistique et de Machine Learning qui vise à prédire une valeur numérique continue à partir d’un ensemble de variables d’entrée.
Contrairement à la classification, qui prédit une étiquette (ex: “spam” / “non spam”, “chat” / “chien”), la régression nous donne un nombre.
Exemples concrets :
- Immobilier : Prédire le prix d’une maison en fonction de sa surface, du nombre de chambres et de son emplacement.
- Marketing : Estimer le chiffre d’affaires futur en fonction des budgets publicitaires sur différents canaux.
- Météo : Prévoir la température maximale de demain en se basant sur les données d’aujourd’hui.
- Ressources Humaines : Estimer le salaire d’un employé en fonction de son expérience et de son niveau d’éducation.
2 L’Idée Centrale : Trouver une Relation
La régression fonctionne en essayant de trouver une relation mathématique entre nos variables d’entrée (les “causes”) et notre variable de sortie (l’“effet”).
Pour cela, on définit deux types de variables :
- Variable Dépendante (Y) : C’est la variable cible, celle que nous voulons prédire (ex: le prix de la maison).
- Variable(s) Indépendante(s) (X) : Ce sont les variables que nous utilisons pour faire la prédiction (ex: la surface, le nombre de chambres). On les appelle aussi prédicteurs ou features.
L’objectif est de construire une fonction mathématique \(f\) telle que \(Y \approx f(X)\). Graphiquement, cela revient à essayer de tracer une ligne ou une courbe qui passe “au mieux” à travers un nuage de points.
3 Les Deux Saveurs Principales de la Régression Linéaire
Le type de régression le plus fondamental est la régression linéaire, qui suppose que la relation entre les variables X et Y est une ligne droite.
3.1 Régression Linéaire Simple
C’est le cas le plus basique : nous n’avons qu’une seule variable indépendante pour prédire notre variable dépendante. Le modèle cherche la meilleure ligne droite possible, décrite par l’équation bien connue : \[Y = aX + b + \varepsilon\]
3.2 Régression Linéaire Multiple
C’est le cas le plus courant et le plus réaliste : nous utilisons plusieurs variables indépendantes pour prédire la variable dépendante. Le modèle cherche alors à combiner l’influence de toutes ces variables. L’équation devient : \[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p + \varepsilon\] Cela nous permet de construire des modèles beaucoup plus riches et précis.
5 À Quoi Sert la Régression ?
La régression a deux super-pouvoirs :
- Prédire 🔮 : Son utilité la plus évidente est de faire des prévisions sur de nouvelles données. Si nous avons un modèle qui lie la surface d’une maison à son prix, nous pouvons estimer le prix d’une nouvelle maison qui arrive sur le marché.
- Comprendre 💡 : La régression n’est pas qu’une boule de cristal. Les coefficients du modèle (\(\beta_1, \beta_2\), etc.) nous renseignent sur la force et la direction de la relation entre chaque variable et la cible. Cela nous permet de répondre à des questions comme : “De combien d’euros le prix augmente-t-il, en moyenne, pour chaque mètre carré supplémentaire ?”.
6 Conclusion
La régression est un outil fondamental de la boîte à outils du data scientist et de l’analyste. Elle fournit un cadre puissant pour modéliser et comprendre les relations entre les variables afin de prédire des résultats numériques. C’est la base de très nombreux modèles plus complexes en Machine Learning.
Maintenant que nous avons une vision d’ensemble de ce qu’est la régression, il est temps de plonger dans la mécanique. Dans notre prochain article, nous aborderons en détail la régression linéaire multiple, en explorant sa formulation mathématique, la méthode des moindres carrés et comment évaluer sa performance.
7 Exercices
Exercise 1
Quelle loi de probabilité est souvent appelée la “reine des distributions” en statistique et est utilisée pour le Z-test ?
La loi de Student est particulièrement utile lorsque :
Dans un test statistique, si la statistique de test suit une loi de Student avec 20 degrés de liberté, cela indique généralement que :
Pour quel type de test la loi du Chi-carré est-elle principalement utilisée ?
La statistique d’un test du Chi-carré est calculée en fonction de :
Dans quel contexte utilise-t-on principalement la loi de Fisher ?
Si vous effectuez une ANOVA pour comparer les moyennes de 4 groupes et que chaque groupe contient 10 observations, quels sont les degrés de liberté de la loi de Fisher associée ?
Lequel des graphiques suivants est le plus approprié pour visualiser la distribution d’une statistique qui suit une loi du Chi-carré avec 5 degrés de liberté ?
Dans le contexte d’un test d’hypothèse, la p-value est calculée à partir de :
Vous effectuez un test pour comparer la moyenne d’un échantillon à une valeur théorique, et vous obtenez une p-value de 0.03. Si vous utilisez un seuil de significativité de 0.05, quelle est votre conclusion ?
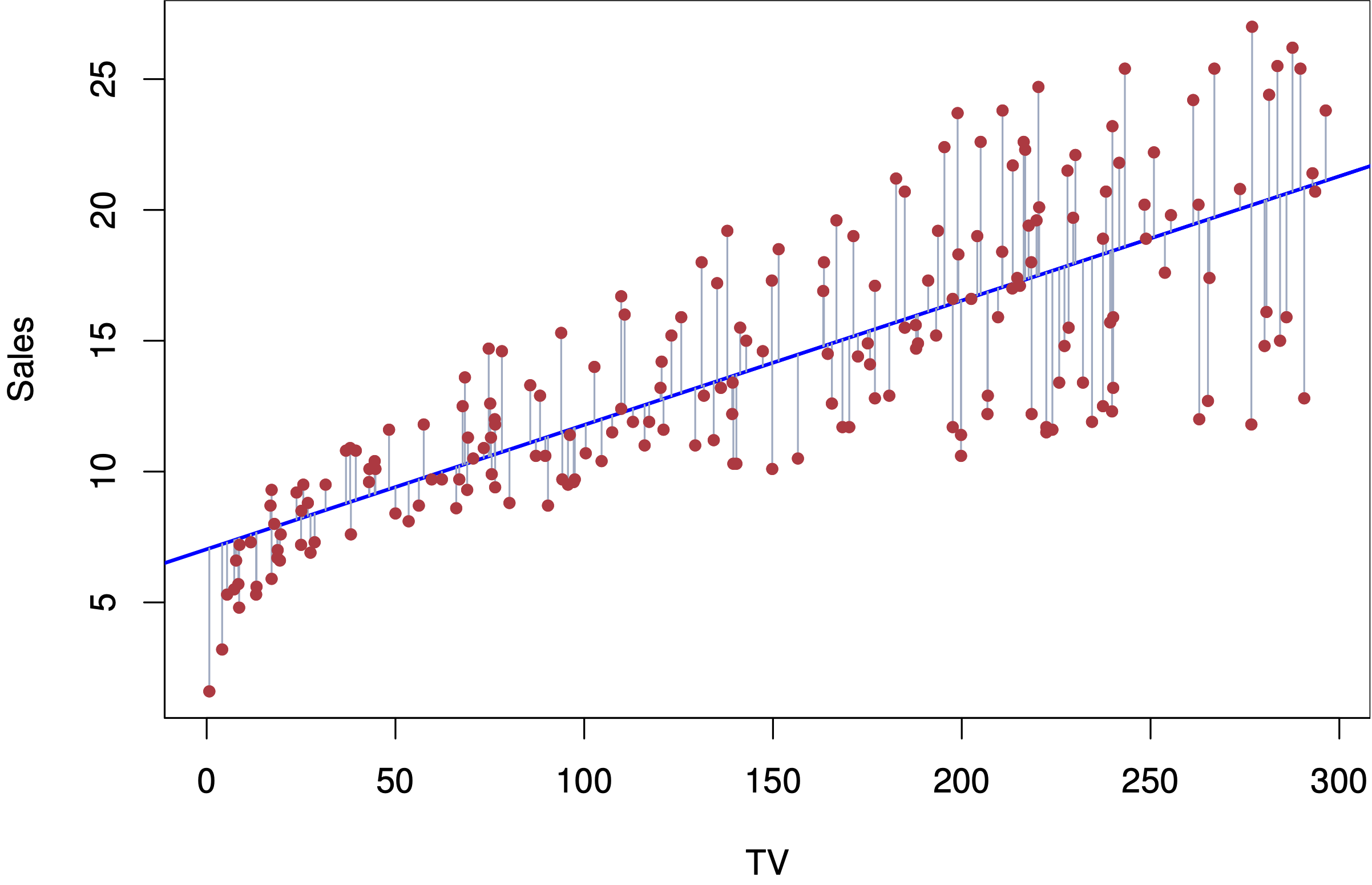
4 Comment le Modèle “Apprend”-il ?
Comment un ordinateur trouve-t-il la “meilleure” ligne à tracer ?
L’idée est de trouver la ligne qui est la plus proche possible de tous les points de données en même temps. Pour chaque point, on mesure l’erreur (appelée résidu), qui est la distance verticale entre le point et la ligne de régression.
Le modèle “apprend” en ajustant les paramètres de la ligne (la pente et l’ordonnée à l’origine) de manière à ce que la somme de toutes ces erreurs au carré soit la plus petite possible. C’est la fameuse méthode des “moindres carrés ordinaires” (MCO), que nous détaillerons dans notre prochain post.