Introduction à la Classification Supervisée : Prédire les Catégories

1 Introduction

Dans nos séries précédentes, nous nous sommes concentrés sur la régression, dont l’objectif est de prédire une valeur numérique continue en répondant à la question “Combien ?”. Nous allons maintenant aborder l’autre pilier de l’apprentissage supervisé : la classification.

L’objectif de la classification est de répondre à une question de type “Lequel ?” ou “À quelle catégorie cela appartient-il ?”. C’est une tâche omniprésente dans notre quotidien, de la détection de spams dans nos emails à la reconnaissance faciale sur nos téléphones.

Ce post a pour but de poser les fondations théoriques et pratiques de la classification. Nous allons formaliser le problème, définir le vocabulaire et, surtout, explorer la boîte à outils essentielle pour évaluer la performance d’un modèle de classification.

2 Formalisation du Problème de Classification

En apprentissage supervisé, nous partons d’un jeu de données, ou échantillon, noté : \[ D_n = \left\{(x_i, y_i)\right\}_{i=1}^n \] Ce jeu de données est constitué de \(n\) paires d’observations, où pour chaque individu \(i\) :

• \(x_i \in \mathcal{X}\) est le vecteur des variables explicatives (features).
• \(y_i \in \mathcal{Y}\) est l’étiquette (label), la catégorie que nous voulons prédire.

On suppose que ces paires \((x_i, y_i)\) sont des réalisations d’un couple de variables aléatoires \((X, Y)\) suivant une distribution de probabilité jointe \(p_{X,Y}\) qui nous est inconnue.

L’Objectif de la Classification

Le but est d’utiliser l’échantillon \(D_n\) pour apprendre une fonction \(f: \mathcal{X} \to \mathcal{Y}\), appelée classifieur, qui est capable d’assigner la bonne étiquette de classe \(y\) à une nouvelle entrée \(x\) non observée.

3 Types de Classification

La nature de l’espace des étiquettes \(\mathcal{Y}\) définit le type de problème :

• Classification Binaire : Il n’y a que deux classes possibles. Par convention, on note \(\mathcal{Y} = \{0, 1\}\) ou \(\mathcal{Y} = \{-1, 1\}\). C’est le cas le plus courant.

  • Exemples : Spam/Non-Spam, Malade/Sain, Client va résilier/Ne va pas résilier.

• Classification Multi-classes : Il y a \(K > 2\) classes possibles. On note \(\mathcal{Y} = \{c_1, c_2, \dots, c_K\}\).

  • Exemples : Reconnaissance de chiffres (10 classes), classification d’articles de presse (Sport, Politique, Économie).

4 Le Classifieur Idéal : Le Classifieur de Bayes

Avant de construire des modèles, demandons-nous : quel serait le meilleur classifieur possible en théorie ? C’est le classifieur de Bayes.

Pour une nouvelle observation \(x\), le classifieur de Bayes choisit la classe \(k\) qui maximise la probabilité conditionnelle a posteriori : \[ f_{\text{Bayes}}(x) = \underset{k \in \mathcal{Y}}{\operatorname{argmax}} P(Y=k | X=x) \] En d’autres termes, il choisit la classe la plus probable, étant donné les caractéristiques de l’observation. Ce classifieur atteint le plus faible taux d’erreur possible.

Le problème : Ce classifieur est un idéal théorique car, en pratique, nous ne connaissons pas la vraie distribution de probabilité \(p_{X,Y}\) qui nous permettrait de calculer \(P(Y=k | X=x)\). Tout l’enjeu de l’apprentissage supervisé est donc de construire un classifieur \(f\) à partir de nos données \(D_n\) qui approxime au mieux ce classifieur de Bayes.

5 Évaluer la Performance : La Boîte à Outils du Classifieur

Comment savoir si notre classifieur est performant ? Contrairement à la régression où l’on utilise souvent une seule métrique (comme le \(R^2\) ou la \(RMSE\)), l’évaluation en classification nécessite une boîte à outils plus riche, surtout pour les problèmes binaires.

5.1 Mesure Générale : L’Exactitude (Accuracy)

L’exactitude est la mesure la plus simple : c’est la proportion de prédictions correctes. \[ \text{Accuracy} = \dfrac{\text{Nombre de prédictions correctes}}{\text{Nombre total de prédictions}} \] Le piège : L’exactitude peut être très trompeuse, en particulier si les classes sont déséquilibrées. Si \(99\%\) de vos emails ne sont pas des spams, un classifieur naïf qui prédit “non spam” pour tous les emails aura une exactitude de \(99\%\), alors qu’il est complètement inutile !

5.2 La Boîte à Outils pour la Classification Binaire

Pour une analyse fine, on utilise la matrice de confusion. Elle croise les prédictions du modèle avec les vraies valeurs.

Matrice de confusion

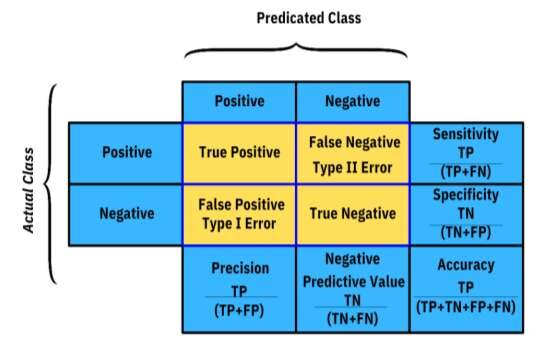
• Vrais Positifs (VP / TP) : Le modèle prédit “Positif” et c’est correct.
• Vrais Négatifs (VN / TN) : Le modèle prédit “Négatif” et c’est correct.
• Faux Positifs (FP / FP) : Le modèle prédit “Positif” mais se trompe (Erreur de Type I).
• Faux Négatifs (FN / FN) : Le modèle prédit “Négatif” mais se trompe (Erreur de Type II).

À partir de cette matrice, on définit des métriques beaucoup plus informatives :

• Précision : “Quand mon modèle dit ‘Positif’, a-t-il raison ?” \[ \text{Précision} = \dfrac{VP}{VP + FP} \] Cruciale quand le coût d’un Faux Positif est élevé (ex: diagnostiquer un cancer à un patient sain).

• Rappel (ou Sensibilité) : “Sur tous les vrais ‘Positifs’ qui existent, combien mon modèle en a-t-il trouvé ?” \[ \text{Rappel} = \dfrac{VP}{VP + FN} \] Cruciale quand le coût d’un Faux Négatif est élevé (ex: rater un email de spam important, ou un patient réellement malade).

• Score F1 : C’est la moyenne harmonique de la précision et du rappel. C’est une excellente métrique pour avoir une vision équilibrée de la performance, surtout si les classes sont déséquilibrées. \[F_1 = 2 \times \dfrac{\text{Précision} \times \text{Rappel}}{\text{Précision} + \text{Rappel}}\]

5.3 Courbe ROC et Score AUC

Pour les classifieurs qui prédisent une probabilité (comme la régression logistique), on peut faire varier le seuil de décision (ex: prédire “Positif” si proba > 0.5, ou > 0.7, etc.).

• La Courbe ROC (Receiver Operating Characteristic) visualise la performance du modèle à tous les seuils. Elle trace le Taux de Vrais Positifs (Rappel) en fonction du Taux de Faux Positifs. Un bon modèle a une courbe qui monte rapidement vers le coin supérieur gauche.

• Le Score AUC (Area Under the Curve) résume cette courbe en un seul chiffre. Il représente la probabilité que le modèle classe une observation positive au hasard plus haut qu’une observation négative au hasard.

  • AUC = 0.5 : Le modèle est aussi bon qu’un tirage au sort.
  • AUC = 1.0 : Le modèle est un classifieur parfait.

6 Conclusion

Nous avons posé les bases de la classification supervisée. Nous avons formalisé le problème et, plus important encore, nous avons découvert la richesse des outils à notre disposition pour évaluer un classifieur.

Le choix de la bonne métrique d’évaluation dépend toujours du contexte de votre problème. Il n’y a pas de “meilleure” métrique universelle. Comprendre la différence entre précision, rappel et AUC est une compétence fondamentale pour tout data scientist.

Et maintenant ?

Maintenant que nous savons comment évaluer un classifieur, il est temps d’en construire un ! Dans notre prochain article, nous aborderons le modèle de classification le plus fondamental et le plus utilisé : la régression logistique.

7 Exercices

Exercise 1  

Question 1

Quel est l’objectif principal de la classification en apprentissage supervisé ?

1. Prédire une valeur numérique continue.
2. Regrouper des données similaires en clusters.
3. Prédire une étiquette de catégorie pour une nouvelle observation.
4. Réduire le nombre de variables dans un jeu de données.

Question 2

Dans quel cas la métrique d’exactitude (accuracy) peut-elle être particulièrement trompeuse ?

1. Lorsque le nombre de variables est très élevé.
2. Lorsque les classes sont déséquilibrées.
3. Lorsque le jeu de données est très petit.
4. Pour les problèmes de classification multi-classes uniquement.

Question 3

Dans une matrice de confusion pour un problème de détection de spam, qu’est-ce qu’un "Faux Positif" (FP) ?

1. Un email de spam que le modèle a correctement identifié comme spam.
2. Un email légitime que le modèle a incorrectement classé comme spam.
3. Un email de spam que le modèle a raté (classé comme légitime).
4. Un email légitime que le modèle a correctement identifié comme légitime.

Question 4

Laquelle de ces métriques répond à la question : "Sur tous les vrais ‘Positifs’ qui existent, combien mon modèle en a-t-il trouvé ?"

1. La Précision (Precision)
2. Le Rappel (Recall / Sensibilité)
3. Le Score F1
4. L’Exactitude (Accuracy)

Question 5

Dans un contexte de diagnostic médical pour une maladie grave, où rater un patient malade a des conséquences dramatiques, quelle métrique est la plus cruciale à maximiser ?

1. La Précision (Precision)
2. Le Rappel (Recall)
3. Le Taux de Faux Positifs
4. L’Exactitude (Accuracy)

Question 6

Qu’est-ce que le score F1 ?

1. La moyenne arithmétique de la précision et du rappel.
2. Le produit de la précision et du rappel.
3. La moyenne harmonique de la précision et du rappel, utile pour avoir une vision équilibrée.
4. Le ratio entre les Vrais Positifs et l’ensemble des prédictions positives.

Question 7

Que représente la courbe ROC (Receiver Operating Characteristic) ?

1. La Précision en fonction du Rappel pour différents seuils.
2. Le Taux de Vrais Positifs en fonction du Taux de Faux Positifs pour différents seuils.
3. L’évolution de l’erreur du modèle en fonction du nombre d’itérations.
4. La distribution des probabilités prédites par le modèle.

Question 8

Un score AUC (Area Under the Curve) de 0.5 signifie que :

1. Le modèle est parfait.
2. Le modèle est inutile, ses prédictions sont équivalentes à un tirage au sort.
3. Le modèle a une exactitude de 50%.
4. Le modèle a une précision de 50% et un rappel de 50%.

Question 9

Quel est le principe du classifieur de Bayes, considéré comme le classifieur idéal ?

1. Il choisit la classe qui a la plus grande probabilité a priori \(P(Y=k)\).
2. Il choisit la classe qui maximise la probabilité conditionnelle a posteriori \(P(Y=k | X=x)\).
3. Il minimise la somme des carrés des erreurs.
4. Il sépare les données avec la plus grande marge possible.

Question 10

Prédire si une image contient un "chat", un "chien" ou un "oiseau" est un exemple de :

1. Classification binaire.
2. Régression.
3. Clustering.
4. Classification multi-classes.

Question 11

Quelle est la principale différence entre la classification et la régression ?

1. La classification prédit des valeurs continues, tandis que la régression prédit des catégories.
2. La classification utilise des données étiquetées, tandis que la régression utilise des données non étiquetées.
3. La classification prédit des catégories, tandis que la régression prédit des valeurs continues.
4. La classification fonctionne uniquement avec des données textuelles, tandis que la régression fonctionne avec des données numériques.

Question 12

Dans un problème de classification binaire, si un modèle a une précision de 0.8 et un rappel de 0.6, que vaut le score F1 ?

1. 0.48
2. 0.7
3. 0.686
4. 0.9

Question 13

Lequel des énoncés suivants décrit le mieux l’objectif du score AUC dans l’évaluation d’un modèle de classification ?

1. Mesurer la proportion de prédictions correctes faites par le modèle.
2. Évaluer la capacité du modèle à séparer les classes en fonction des probabilités prédites.
3. Calculer la moyenne harmonique entre la précision et le rappel du modèle.
4. Déterminer le seuil optimal de probabilité pour prendre une décision de classification.

Question 14

Dans un problème de classification multi-classes, un modèle a une matrice de confusion. Comment calcule-t-on l’exactitude globale du modèle ?

1. En faisant la moyenne des précisions de chaque classe.
2. En faisant la moyenne des rappels de chaque classe.
3. En divisant la somme des éléments de la diagonale (prédictions correctes) par le nombre total de prédictions.
4. En calculant la moyenne harmonique des précisions et rappels de chaque classe.

Question 15

Pourquoi est-il important de diviser les données en ensembles d’entraînement et de test avant de construire un modèle de classification ?

1. Pour augmenter la taille de l’ensemble de données et améliorer les performances du modèle.
2. Pour s’assurer que le modèle est entraîné sur toutes les données disponibles.
3. Pour évaluer les performances du modèle sur des données qu’il n’a jamais vues, simulant ainsi son comportement en production.
4. Pour faciliter l’interprétation des résultats du modèle.