L’Analyse en Composantes Principales (ACP) : Un Guide Complet

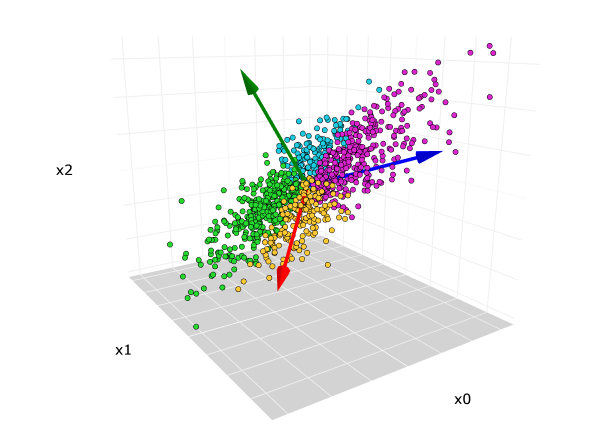
1 Introduction : Résumer l’Information Efficacement

Face à un jeu de données avec des dizaines, voire des centaines de variables, comment peut-on en extraire l’essence ? L’Analyse en Composantes Principales (ACP ou PCA) est la technique reine pour répondre à cette question. C’est un algorithme non supervisé et linéaire qui transforme un grand nombre de variables corrélées en un plus petit nombre de nouvelles variables, non corrélées, appelées composantes principales.

Ce guide vous mènera de l’intuition géométrique à la formalisation mathématique, puis à l’application pratique en Python, en insistant sur l’analyse conjointe des individus et des variables pour une interprétation complète.

2 L’Intuition Géométrique : Trouver le Meilleur Angle de Vue

Imaginez un nuage de points en 3D. Pour le représenter en 2D (sur une feuille de papier), vous chercheriez le meilleur angle de vue pour que sa projection (son “ombre”) soit la plus étalée possible, conservant ainsi un maximum d’information sur sa forme.

Le PCA fait exactement cela : il cherche séquentiellement les axes de plus grande variance dans les données.

• La 1ère composante principale (PC1) est la direction qui maximise la variance des données projetées. C’est l’axe “le plus long” du nuage de points.
• La 2ème composante principale (PC2) est la direction, orthogonale à PC1, qui maximise la variance restante.
• Et ainsi de suite pour les autres composantes.

3 Formalisation Mathématique du Problème ⚙️

Soit \(X\) notre matrice de données, avec \(n\) individus (lignes) et \(p\) variables (colonnes).

1. Centrage et Réduction : L’ACP est très sensible à l’échelle des variables. On travaille donc quasi systématiquement sur les données centrées et réduites.

   • On centre les données : \(Y = X - 1_n\bar{x}^T\), où chaque colonne de \(Y\) a une moyenne de 0.
   • On réduit les données : \(Z\) est la matrice où chaque colonne de \(Y\) a été divisée par son écart-type. Les colonnes de \(Z\) ont donc une moyenne de 0 et une variance de 1.

2. La Matrice de Covariance/Corrélation : Le but étant de maximiser la variance, on s’intéresse à la matrice qui résume les variances et covariances des variables. Sur des données centrées-réduites \(Z\), la matrice de covariance est identique à la matrice de corrélation, notée \(R\): \[ R = \frac{1}{n-1} Z^T Z \]

3. Le Cœur de l’ACP : Diagonalisation L’ACP consiste à trouver les axes d’un nouveau repère où la variance est maximisée et les covariances sont nulles. Mathématiquement, cela revient à diagonaliser la matrice de corrélation \(R\).

   Les composantes principales sont les vecteurs propres (eigenvectors) de la matrice \(R\). La variance expliquée par chaque composante principale est l’eigenvalue (valeur propre) correspondante.

   Soit \((\lambda_1, v_1), (\lambda_2, v_2), \dots, (\lambda_p, v_p)\) les paires (valeur propre, vecteur propre) de \(C\), triées par ordre décroissant de valeur propre (\(\lambda_1 \ge \lambda_2 \ge \dots \ge 0\)).

   • Le vecteur \(v_1\) définit la direction de la 1ère composante principale (PC1).
   • La valeur \(\lambda_1\) est la variance portée par cet axe.
   • Les coordonnées des individus sur ce nouvel axe sont obtenues en projetant \(Z\) sur \(v_1\).

La proportion de variance totale expliquée par la \(k\)-ième composante est : \[ \text{Variance Expliquée}_k = \dfrac{\lambda_k}{\sum_{j=1}^{p} \lambda_j} = \dfrac{\lambda_k}{p} \] (Car la trace de la matrice de corrélation est égale à \(p\)).

4 Représentations Graphiques

4.1 Représentation Graphique des Individus

Le premier objectif de l’ACP est souvent de visualiser les individus. Pour cela, on les projette sur le premier plan principal, c’est-à-dire le plan formé par les deux premières composantes principales (PC1 et PC2), qui capturent le maximum de la variance totale.

Comment interpréter le graphique des individus ?

1. Proximité entre les points : Deux individus qui sont proches sur le graphique ont des profils similaires sur l’ensemble des variables. Inversement, deux individus éloignés sont très différents.
2. Distance par rapport à l’origine : L’origine (0,0) représente l’individu “moyen”. Plus un point est éloigné de l’origine, plus son profil est atypique.
3. Position sur les axes : La position d’un individu sur un axe (par exemple, un score élevé sur PC1) indique sa contribution à cette composante. L’interprétation de cette position se fait en conjonction avec le cercle de corrélation (voir section suivante) : si PC1 est l’axe de la “taille”, un individu avec une coordonnée positive élevée sur PC1 est un individu “grand”.

Utilisation de variables supplémentaires :

Une technique très puissante consiste à colorer les points en fonction d’une variable qualitative supplémentaire qui n’a pas participé à la construction des axes (par exemple, une catégorie de produit, une classe de maladie, une région géographique). Cela permet de voir si des groupes naturels se forment et si les composantes principales séparent bien ces groupes.

La qualité de la représentation de chaque individu sur le plan est mesurée par son cosinus carré (cos²) cumulé sur les deux axes. Un cos² élevé (proche de 1) signifie que l’individu est bien représenté sur ce plan. On peut visualiser cette qualité en faisant varier la taille ou l’intensité de la couleur des points.

4.2 Représentation Graphique des Variables

Après avoir visualisé les individus, il est crucial de comprendre ce que nos nouvelles dimensions (PC1, PC2) signifient. Pour cela, on utilise le cercle de corrélation.

Ce graphique représente les variables originales dans le nouvel espace créé par les composantes principales. La coordonnée de chaque variable sur un axe est simplement sa corrélation avec cet axe.

Comment interpréter le cercle de corrélation ?

1. Proximité du cercle : Une variable dont le point est proche du bord du cercle est bien représentée par le plan principal. Son information a été bien conservée. À l’inverse, une variable proche du centre (0,0) est mal représentée sur ce plan.

2. Corrélation avec les axes : La projection d’une variable sur un axe mesure sa corrélation avec celui-ci.

   • Une variable très à droite (ou à gauche) est fortement corrélée (positivement ou négativement) avec PC1.
   • Une variable très en haut (ou en bas) est fortement corrélée avec PC2.

3. Angles entre les variables : L’angle entre les vecteurs représentant deux variables nous renseigne sur leur corrélation originale.

   • Angle aigu (< 90°) : Les deux variables sont positivement corrélées.
   • Angle obtus (> 90°) : Les deux variables sont négativement corrélées.
   • Angle droit (≈ 90°) : Les deux variables ne sont pas corrélées.

C’est en analysant ce cercle que l’on peut donner un sens métier aux axes (ex: PC1 est “l’axe de la taille”, PC2 est “l’axe de la texture”, etc.).

4.3 Double Représentation Graphique

La véritable puissance de l’analyse en composantes principales réside dans la superposition et l’interprétation conjointe du graphique des individus et du cercle de corrélation. C’est ce qu’on appelle un biplot.

L’idée est d’interpréter la position d’un individu par rapport aux variables.

1. Un individu (point) sera fortement caractérisé par un groupe de variables si son point est proche des vecteurs de ces variables.
2. Un individu aura une valeur élevée pour une variable si sa projection sur le vecteur de cette variable est loin de l’origine dans la même direction.
3. Inversement, un individu aura une valeur faible pour une variable si sa projection est loin de l’origine dans la direction opposée du vecteur.
4. Un individu dont la projection sur un axe est proche de l’origine est “moyen” pour cette variable.

Exemple avec nos données sur le cancer : * Le graphique des individus montre les tumeurs malignes à droite (PC1 > 0). * Le cercle de corrélation montre que des variables comme mean radius et mean perimeter sont fortement corrélées à PC1 (leurs vecteurs pointent vers la droite). * Conclusion croisée : Les tumeurs malignes sont donc caractérisées par des valeurs élevées de rayon moyen, de périmètre moyen, etc. Ce qui est tout à fait logique. L’ACP a réussi à capturer cette structure et nous permet de l’interpréter visuellement.

5 Atelier Pratique : L’Analyse Complète

Nous allons appliquer une ACP complète sur le jeu de données breast_cancer (30 variables) pour visualiser les individus et interpréter les variables.

5.1 Prérequis : Chargement et Mise à l’Échelle

Règle d’Or du PCA

Avant d’appliquer un PCA, vous devez impérativement mettre vos variables à la même échelle, généralement en utilisant la standardisation (StandardScaler).

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# 1. Données (X)
cancer = load_breast_cancer()
X, y = cancer.data, cancer.target
feature_names = cancer.feature_names
target_names = cancer.target_names
n, p = X.shape

# 2. Données centrées-réduites (Z)
scaler = StandardScaler()
Z = scaler.fit_transform(X)

# 3. Appliquer le PCA
pca = PCA()
C = pca.fit_transform(Z) # C contient les coordonnées des individus sur les nouvelles composantes

5.2 Étape 1 : Combien de Dimensions Garder ? (Scree Plot)

Le “scree plot” ou graphique des éboulis nous aide à choisir le nombre de composantes à retenir en visualisant la variance expliquée par chacune.

explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_variance_ratio)

print(f"Variance expliquée par les 2 premières composantes: {cumulative_variance[1]:.2%}")

plt.figure(figsize=(10, 7))
plt.bar(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, alpha=0.5, align='center', label='Variance individuelle')
plt.step(range(1, len(cumulative_variance) + 1), cumulative_variance, where='mid', label='Variance cumulée')
plt.xlabel('Nombre de Composantes Principales')
plt.ylabel('Proportion de Variance Expliquée')
plt.title('Graphique des Éboulis (Scree Plot)')
plt.axhline(y=0.95, color='r', linestyle='--', label='Seuil de 95%')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Variance expliquée par les 2 premières composantes: 63.24%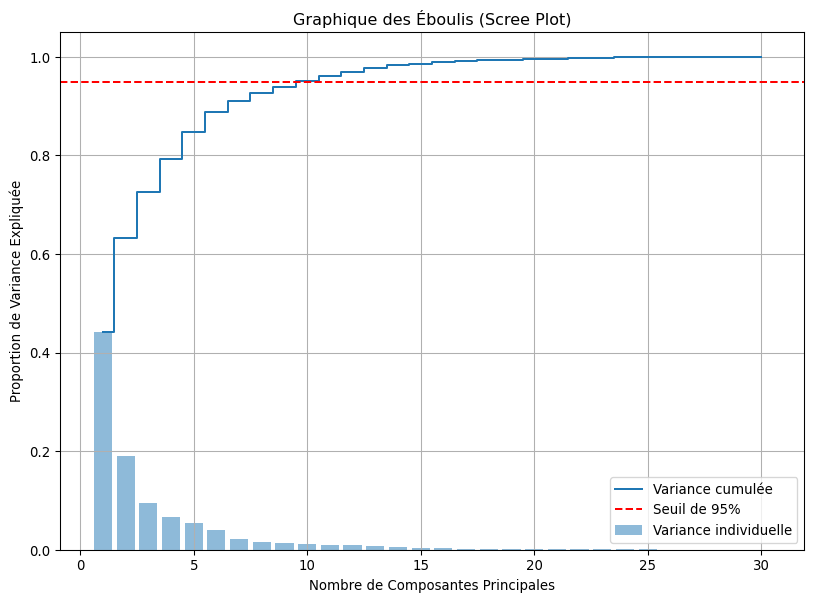

Le graphique confirme que 2 composantes capturent environ 63% de l’information, et qu’il en faut environ 10 pour dépasser 95%. Pour la visualisation, nous nous contenterons des deux premières.

5.3 Étape 2 : Analyse des Individus (Projection Plot)

Visualisons les individus (les tumeurs) sur le premier plan principal (PC1, PC2).

# Créer un DataFrame pour la visualisation
pca_df = pd.DataFrame(data=C[:, :2], columns=['PC1', 'PC2'])
pca_df['label'] = pd.Series(y).map({0: target_names[0], 1: target_names[1]})

# Visualisation
plt.figure(figsize=(12, 9))
sns.scatterplot(x='PC1', y='PC2', hue='label', data=pca_df, palette='viridis', s=100, alpha=0.8)
plt.title('Projection des Individus sur le Premier Plan Principal')
plt.xlabel(f'PC1 ({explained_variance_ratio[0]:.2%} de variance)')
plt.ylabel(f'PC2 ({explained_variance_ratio[1]:.2%} de variance)')
plt.legend(title='Diagnostic')
plt.grid(True)
plt.show()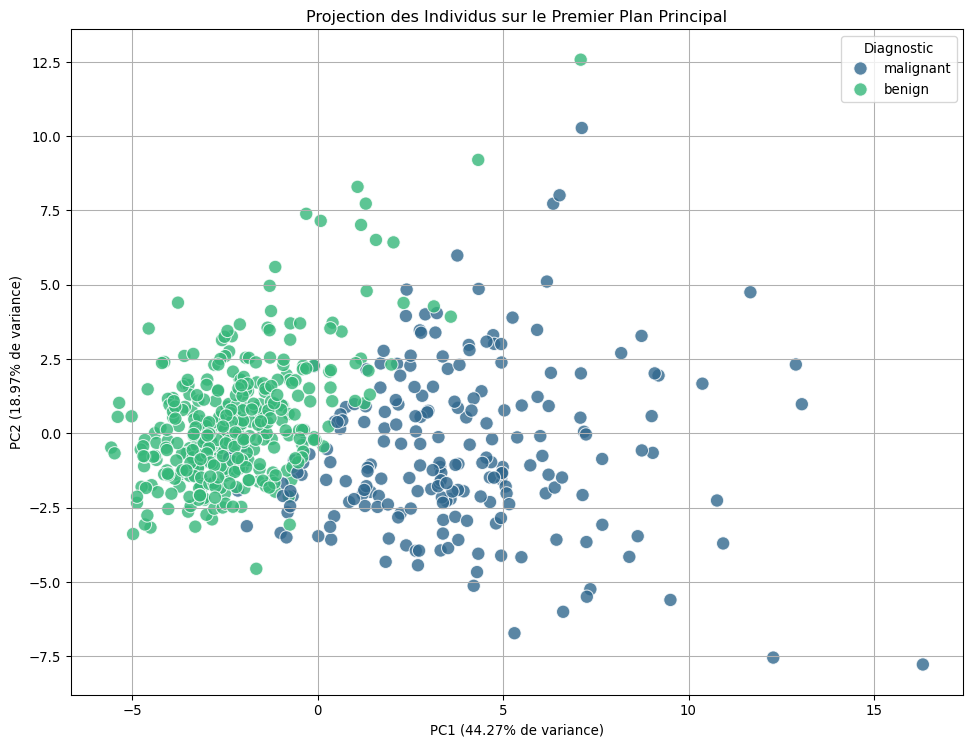

Observation : Les deux classes de tumeurs (malignes et bénignes) sont remarquablement bien séparées sur ce plan, suggérant une structure sous-jacente forte dans les données.

5.4 Étape 3 : Analyse des Variables (Cercle de Corrélation)

Pour comprendre ce que signifient PC1 et PC2, nous devons regarder comment les variables originales sont corrélées avec ces nouveaux axes. C’est le rôle du cercle de corrélation.

Comment l’interpréter ?

• Proximité du cercle : Une variable proche du cercle est bien représentée par le plan PC1/PC2.
• Direction : La projection d’une variable sur un axe indique sa corrélation avec cet axe. Une variable proche de l’axe horizontal est fortement corrélée à PC1.
• Angles : Des variables proches sont positivement corrélées. Des variables opposées sont négativement corrélées. Des variables à 90° sont peu ou pas corrélées.

# Calcul des corrélations variables-composantes
# (pca.components_.T contient les vecteurs propres)
# (np.sqrt(pca.explained_variance_) est l'écart-type de chaque composante)
df_corr = pd.DataFrame(pca.components_.T * np.sqrt(pca.explained_variance_),
                       columns=[f'PC{i+1}' for i in range(p)],
                       index=feature_names)

# Cercle de corrélation
fig, ax = plt.subplots(figsize=(12, 12))
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.axhline(0, color='grey', lw=1)
ax.axvline(0, color='grey', lw=1)
ax.set_xlabel(f'PC1 ({explained_variance_ratio[0]:.2%} de variance)')
ax.set_ylabel(f'PC2 ({explained_variance_ratio[1]:.2%} de variance)')
ax.set_title('Cercle de Corrélation des Variables')

# Dessiner le cercle
circle = plt.Circle((0,0), 1, color='blue', fill=False, linestyle='--')
ax.add_artist(circle)

# Dessiner les flèches pour chaque variable
for i in range(len(feature_names)):
    ax.arrow(0, 0, df_corr.iloc[i, 0], df_corr.iloc[i, 1],
             head_width=0.03, head_length=0.03, fc='r', ec='r')
    ax.text(df_corr.iloc[i, 0] * 1.05, df_corr.iloc[i, 1] * 1.05,
            feature_names[i], color='k', ha='center', va='center')

plt.grid(True)
plt.show()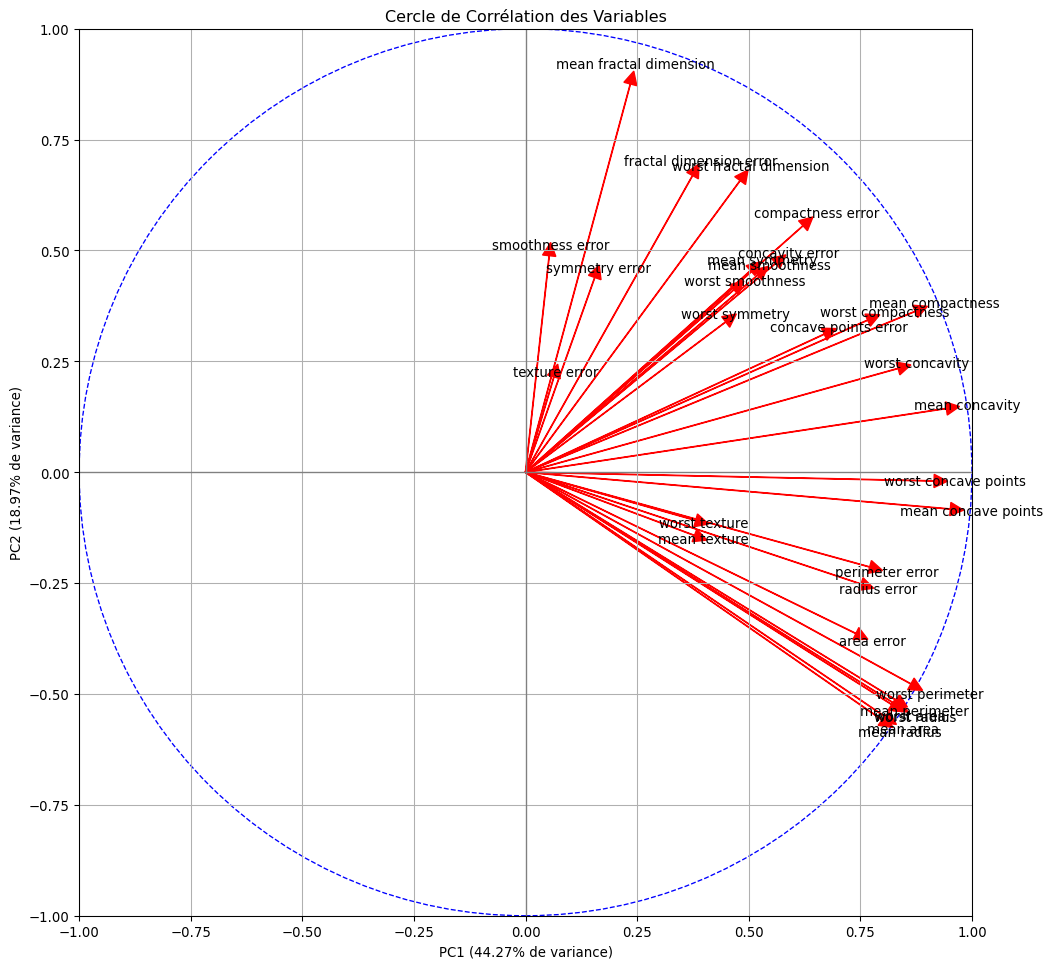

5.5 Étape 4 : Interprétation Croisée et Synthèse 💡

C’est ici que la magie opère, en combinant les informations des deux graphiques.

1. Interpréter les axes grâce au cercle :
   • Axe PC1 (horizontal) : De nombreuses variables comme mean radius, mean perimeter, mean area, worst concave points sont fortement et positivement corrélées à cet axe. Ces variables décrivent toutes la taille et la gravité de la tumeur. On peut donc interpréter PC1 comme un axe de “sévérité/taille tumorale”.
   • Axe PC2 (vertical) : Des variables comme mean texture, mean smoothness et symmetry error sont corrélées (plus faiblement) à cet axe. Il semble représenter une notion de texture ou d’irrégularité de la tumeur.
2. Interpréter la projection des individus grâce aux axes :
   • En regardant le premier graphique, les tumeurs malignes (malignant) se trouvent du côté des valeurs positives de PC1.
   • Conclusion : Les tumeurs malignes sont celles qui ont une valeur élevée sur l’axe de “sévérité/taille tumorale”, ce qui est parfaitement logique d’un point de vue médical. L’ACP a réussi à extraire et à résumer cette information essentielle sur un seul axe.

6 Conclusion

L’Analyse en Composantes Principales est un outil fondamental et polyvalent. C’est votre meilleur allié pour la visualisation exploratoire et pour compresser l’information de vos données.

Ses forces :

• Rapide et efficace.
• Garantit que les nouvelles variables (les composantes) sont décorrélées entre elles.
• Très utile en pré-traitement pour d’autres algorithmes.

Sa principale faiblesse :

• L’interprétabilité. Une composante principale est une combinaison de toutes les variables originales. Il est souvent difficile de lui donner un sens métier clair, contrairement à une variable d’origine comme “l’âge” ou le “revenu”.

Et maintenant ?

Le PCA est un algorithme non supervisé : il ignore complètement les étiquettes de classe pour trouver ses axes. Mais que faire si notre objectif principal est justement de séparer au mieux les classes ? Existe-t-il une méthode de réduction de dimensionnalité qui utilise cette information ? La réponse est oui, et c’est ce que nous découvrirons dans notre prochain article sur l’Analyse Discriminante Linéaire (LDA).

7 Exercices

Exercise 1  

Question 1

Quel est l’objectif principal de l’Analyse en Composantes Principales (PCA) ?

1. Sélectionner un sous-ensemble des variables originales.
2. Classer les données dans des catégories (apprentissage supervisé).
3. Trouver les directions de plus grande variance dans les données pour les résumer.
4. Prédire une valeur numérique continue.

Question 2

Quelle est l’étape de pré-traitement la plus cruciale avant d’appliquer un PCA ?

1. Supprimer les valeurs aberrantes (outliers).
2. Mettre toutes les variables à la même échelle (par exemple, avec StandardScaler).
3. Convertir toutes les données en nombres entiers.
4. Il n’y a pas besoin de pré-traitement particulier.

Question 3

Comment est définie la première composante principale (PC1) ?

1. C’est la direction la plus corrélée avec la variable cible.
2. C’est la direction dans l’espace qui capture le maximum de la variance des données.
3. C’est une variable originale choisie au hasard.
4. C’est la direction qui minimise la variance des données.

Question 4

Quelle est la relation géométrique entre la première (PC1) et la deuxième (PC2) composante principale ?

1. Elles sont parallèles.
2. Elles sont identiques.
3. Elles sont orthogonales (à 90° l’une de l’autre).
4. Il n’y a pas de relation définie entre elles.

Question 5

Qu’est-ce que le “graphique de la variance expliquée cumulée” nous aide à faire ?

1. À choisir le bon algorithme de classification.
2. À déterminer le nombre de composantes principales à conserver.
3. À visualiser les clusters dans les données.
4. À interpréter le sens métier de chaque composante.

Question 6

Quel est le principal inconvénient de l’ACP (PCA) ?

1. L’algorithme est très lent, même sur de petits jeux de données.
2. Les nouvelles variables (composantes) créées sont souvent difficiles à interpréter.
3. Il ne fonctionne que pour la visualisation en 2D.
4. Il nécessite des données étiquetées pour fonctionner (supervisé).

Question 7

L’ACP (PCA) est une technique…

1. …supervisée et linéaire.
2. …non supervisée et non-linéaire.
3. …supervisée et non-linéaire.
4. …non supervisée et linéaire.

Question 8

Dans l’atelier pratique, qu’a révélé la visualisation des données du cancer du sein après réduction à 2 dimensions par PCA ?

1. Que les données formaient un seul grand groupe homogène.
2. Que les deux classes (tumeurs malignes et bénignes) étaient bien séparées dans le nouvel espace.
3. Que le PCA n’a pas réussi à réduire la dimension.
4. Que la première composante principale était identique à la variable “taille de la tumeur”.

Question 9

Qu’est-ce qu’une composante principale ?

1. C’est une des variables originales du jeu de données.
2. C’est une combinaison linéaire de toutes les variables originales.
3. C’est un point de donnée choisi comme représentant d’un cluster.
4. C’est une mesure de l’erreur du modèle.

Question 10

Dans l’atelier, combien de variance totale des 30 variables originales les 2 premières composantes principales expliquent-elles environ ?

1. 100%
2. Moins de 20%
3. Environ 65%
4. Exactement 50%

Question 11

Que représentent les valeurs propres (eigenvalues) de la matrice de corrélation lors d’une ACP ?

1. Les coordonnées des individus sur les nouveaux axes.
2. La variance expliquée par chaque composante principale.
3. La corrélation entre deux variables originales.
4. La qualité de représentation des variables.

Question 12

Sur le cercle de corrélation, une variable est d’autant mieux représentée par le plan principal (PC1, PC2) que son point est…

1. …proche de l’origine (0,0).
2. …situé sur l’axe PC1.
3. …proche du bord du cercle (de rayon 1).
4. …proche d’un autre point de variable.

Question 13

Sur un biplot (superposition individus/variables), un individu aura une valeur élevée pour une variable donnée si :

1. Son point est loin du vecteur représentant la variable.
2. Sa projection sur le vecteur de la variable est proche de l’origine.
3. Sa projection sur le vecteur de la variable se trouve loin de l’origine, dans la même direction que le vecteur.
4. Son point se situe à l’opposé du vecteur de la variable par rapport à l’origine.

Question 14

Quelle est une propriété mathématique fondamentale des composantes principales (par exemple PC1, PC2, etc.) ?

1. Elles sont toujours positivement corrélées entre elles.
2. Elles sont décorrélées les unes des autres (leur covariance est nulle).
3. Elles ont toutes la même variance.
4. Elles sont plus nombreuses que les variables originales.

Question 15

La qualité de la représentation d’un individu sur un plan factoriel est mesurée par :

1. Sa contribution à la variance de l’axe.
2. Sa distance à l’origine.
3. Son cosinus carré (cos²).
4. Sa corrélation avec les variables.