Introduction à la Réduction de Dimensionnalité : Moins, c’est Souvent Mieux

1 Introduction : Le Problème des Données “Larges”

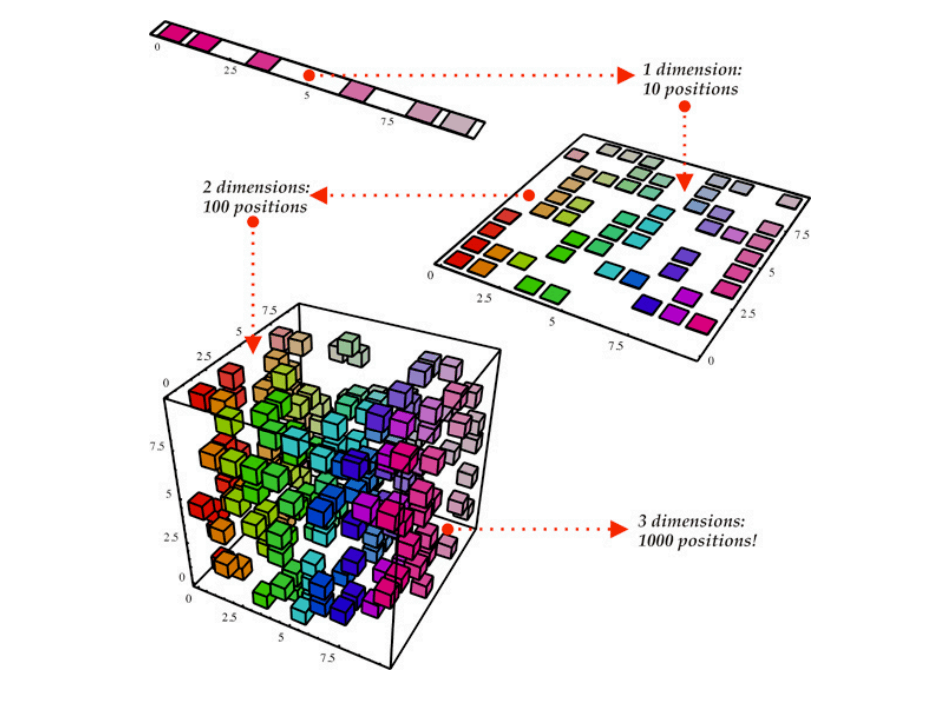
Dans nos explorations du Machine Learning, nous avons appris à construire des modèles prédictifs puissants. Mais tous ces modèles reposent sur une hypothèse : que les données que nous leur fournissons sont de bonne qualité et pertinentes. Que se passe-t-il lorsque nous sommes confrontés à un jeu de données avec des dizaines, des centaines, voire des milliers de variables (ou features) ?

Comment visualiser une relation dans un espace à 50 dimensions ? Comment un algorithme peut-il apprendre efficacement quand l’information pertinente est noyée au milieu d’un grand nombre de variables redondantes ou inutiles ?

C’est le défi posé par les données de grande dimension. Ce post est le premier d’une série dédiée à une famille de techniques essentielles pour relever ce défi : la réduction de dimensionnalité. Nous allons découvrir pourquoi “moins” est souvent synonyme de “mieux” en Machine Learning.

2 Le Fléau de la Haute Dimension (The Curse of Dimensionality)

Ce terme, qui semble tout droit sorti d’un film fantastique, décrit une série de problèmes très réels qui apparaissent lorsque le nombre de dimensions (de variables) d’un jeu de données augmente.

L’intuition est la suivante : plus vous ajoutez de dimensions, plus l’espace de données devient exponentiellement “grand” et “vide”. Vos points de données, même s’ils sont nombreux, deviennent de plus en plus isolés les uns des autres, comme des îles perdues dans un immense océan.

Les Conséquences de la Malédiction

1. La Notion de Distance perd son Sens : Dans un espace à très haute dimension, la distance entre n’importe quelle paire de points devient presque la même. C’est une catastrophe pour les algorithmes basés sur la distance comme k-NN, les SVM et le clustering.
2. Sparsité des Données : Pour couvrir correctement un espace de grande dimension, il faudrait une quantité de données astronomique. Avec un nombre fixe d’observations, vos données deviennent de plus en plus éparses, ce qui rend difficile l’apprentissage de motifs fiables.
3. Augmentation du Risque de Surapprentissage : Avec plus de variables, il y a plus de chances que votre modèle trouve des corrélations fallacieuses dans le bruit de vos données d’entraînement, ce qui nuit à sa capacité de généralisation.

3 Pourquoi Réduire la Dimension ? Les Bénéfices

Réduire la dimensionnalité de nos données n’est pas seulement une optimisation technique, c’est une étape stratégique qui apporte des bénéfices considérables.

• Visualisation de Données : C’est le bénéfice le plus direct. En réduisant des données complexes à 2 ou 3 dimensions, nous pouvons les tracer sur un graphique, les explorer visuellement et découvrir des structures (comme des clusters) qui étaient invisibles auparavant.
• Réduction du Bruit : En éliminant les variables non pertinentes ou redondantes, on “nettoie” le signal, ce qui peut aider les modèles à mieux apprendre.
• Accélération des Algorithmes : Moins de variables signifie des calculs plus simples et donc des temps d’entraînement beaucoup plus courts.
• Lutte contre le Surapprentissage : Un modèle plus simple, avec moins de variables, a moins de chances de sur-apprendre.
• Réduction des Coûts de Stockage : Moins de dimensions signifie des fichiers de données plus légers.

4 Les Deux Grandes Stratégies

Il existe deux approches fondamentales pour réduire la dimensionnalité.

4.1 La Sélection de Caractéristiques (Feature Selection)

• L’Idée : On choisit un sous-ensemble des variables originales les plus importantes et on abandonne les autres.
• L’Analogie : C’est comme faire le tri dans sa bibliothèque et ne garder que les livres les plus pertinents.
• Avantage : C’est simple à comprendre et le modèle final reste très interprétable, car il est basé sur les variables originales.
• Inconvénient : On perd l’information potentiellement contenue dans les variables que l’on a écartées.

4.2 L’Extraction de Caractéristiques (Feature Extraction)

• L’Idée : On ne sélectionne pas de variables, on en crée de nouvelles, moins nombreuses, qui sont des combinaisons des variables originales.
• L’Analogie : C’est comme résumer un livre. On n’a pas gardé quelques chapitres intacts ; on a créé un nouveau texte, plus court, qui capture l’essence de toute l’histoire.
• Avantage : Cette approche préserve une partie de l’information de toutes les variables originales. Elle est souvent plus puissante que la sélection.
• Inconvénient : Les nouvelles variables (appelées “composantes” ou “facteurs latents”) sont des constructions mathématiques et sont généralement moins interprétables que les variables d’origine.

Cette série se concentrera principalement sur cette deuxième approche, l’extraction de caractéristiques.

5 Feuille de Route de la Série

Pour maîtriser l’art de la réduction de dimensionnalité, nous allons explorer les algorithmes les plus importants :

1. L’Analyse en Composantes Principales (ACP / PCA) : Le pilier de la réduction de dimensionnalité linéaire, qui cherche les axes de plus grande variance.
2. L’Analyse Discriminante Linéaire (LDA) : Une alternative supervisée au PCA, qui cherche les axes qui séparent le mieux les classes.
3. t-SNE et UMAP : Les champions de la visualisation non-linéaire, capables de révéler des structures complexes dans les données.
4. Projet de Synthèse : Nous mettrons tout en pratique dans un workflow de Machine Learning complet.

6 Conclusion

La haute dimensionnalité est un défi majeur en science des données, mais ce n’est pas une fatalité. En comprenant ses effets et en maîtrisant les techniques de réduction de dimensionnalité, vous pouvez transformer des jeux de données intimidants et complexes en sources d’informations claires et exploitables.

Et maintenant ?

Maintenant que nous comprenons pourquoi il faut réduire la dimension, plongeons dans le comment. Dans notre prochain article, nous aborderons l’algorithme le plus célèbre et le plus fondamental de cette famille : l’Analyse en Composantes Principales (PCA).

7 Exercices

Exercise 1  

Question 1

Quel est l’objectif principal des techniques de réduction de dimensionnalité ?

1. Augmenter le nombre d’observations dans un jeu de données.
2. Gérer les jeux de données ayant un très grand nombre de variables (features).
3. Prédire une valeur numérique continue.
4. Classer les données dans des catégories prédéfinies.

Question 2

Quelle est l’une des conséquences majeures du “Fléau de la Haute Dimension” ?

1. Les algorithmes deviennent plus rapides.
2. La notion de distance perd son sens car la distance entre deux points quelconques devient très similaire.
3. Le risque de sous-apprentissage (underfitting) augmente.
4. Les données deviennent plus denses et plus faciles à modéliser.

Question 3

Lequel de ces bénéfices est le plus directement lié à la réduction de données à 2 ou 3 dimensions ?

1. La garantie que le modèle sera 100% exact.
2. La possibilité d’explorer visuellement les structures des données, comme les clusters.
3. L’élimination du besoin de nettoyer les données.
4. L’augmentation du nombre de variables.

Question 4

Quelle est la différence fondamentale entre la “Sélection de Caractéristiques” et l’“Extraction de Caractéristiques” ?

1. La sélection crée de nouvelles variables, tandis que l’extraction conserve les variables originales.
2. La sélection choisit un sous-ensemble des variables originales, tandis que l’extraction crée de nouvelles variables en combinant les originales.
3. Il n’y a pas de différence, les termes sont interchangeables.
4. La sélection est supervisée, l’extraction est non supervisée.

Question 5

Quelle approche de réduction de dimensionnalité préserve généralement mieux l’interprétabilité du modèle final ?

1. L’Extraction de Caractéristiques (Feature Extraction).
2. La Sélection de Caractéristiques (Feature Selection).
3. Les deux de manière égale.
4. Aucune des deux.

Question 6

L’article utilise une analogie pour décrire l’Extraction de Caractéristiques. Laquelle ?

1. Trier sa bibliothèque et ne garder que les livres pertinents.
2. Résumer un livre en un texte plus court qui capture son essence.
3. Traduire un livre dans une autre langue.
4. Supprimer des chapitres au hasard dans un livre.

Question 7

Comment la réduction de dimensionnalité aide-t-elle à lutter contre le surapprentissage (overfitting) ?

1. En ajoutant plus de bruit aux données.
2. En rendant le modèle plus complexe.
3. En simplifiant le modèle avec moins de variables, ce qui réduit le risque qu’il apprenne à partir du bruit.
4. En augmentant le nombre d’exemples d’entraînement.

Question 8

Quels types d’algorithmes sont particulièrement vulnérables au “Fléau de la Haute Dimension” en raison de leur dépendance à la notion de distance ?

1. Les arbres de décision.
2. La régression linéaire.
3. k-NN, les SVM et les algorithmes de clustering.
4. Les classifieurs Naive Bayes.

Question 9

Quel est le principal inconvénient des méthodes d’Extraction de Caractéristiques comme l’ACP (PCA) ?

1. Elles sont beaucoup plus lentes que les méthodes de sélection.
2. Elles ne peuvent pas être utilisées pour la visualisation de données.
3. Les nouvelles caractéristiques créées sont souvent difficiles à interpréter.
4. Elles ne fonctionnent que sur des jeux de données avec moins de 10 variables.

Question 10

Quelles sont les deux grandes stratégies de réduction de dimensionnalité présentées dans l’article ?

1. L’augmentation de données et le nettoyage de données.
2. L’apprentissage supervisé et l’apprentissage non supervisé.
3. La Sélection de Caractéristiques et l’Extraction de Caractéristiques.
4. La Régression et la Classification.